고정 헤더 영역
상세 컨텐츠
본문

이전에 고전적 가정(Classical Assumption)의 3번째 assumption을 만족하지 못하는 자기상관성 문제를 다뤘다. 이번에는 Classical Assumption 3번의 2번째 가정을 만족하지 못하는 이분산(Heteroscedasticity)에 대한 내용을 다루려고 한다.
프로그램을 작성하기 이전에, 프로그램 분석에 필요한 통계 개념을 짚고 넘어가자.
[ 이분산 (Heteroscedasticity) ]
Classical Assumption 중 3번째 assumption의 내용은 아래와 같다. (나머지 가정에 대한 내용이 궁금하신 분들은 해당 링크 참고해주세요.)
(3-1) (if )
(3-2) (if )
- (3-1) 만족: 자기상관이 없다. (No Autocorrelation)
- (3-2) 만족: 오차항의 등분산성 가정 충족 → 공분산(Homoscedasticity) 존재
그러나 (3-1)을 만족하지 못하면 오차항에는 자기상관(autocorrelation)이 존재하는 경우로 이미 배웠다. 대부분의 거시 경제 데이터에는 자기상관이 거의 대부분 존재한다고 하였고, 이를 검정하는 방법으로 Durbin-Watson test와 Durbin's h Test를 설명하였다. 해당 개념은 아래의 링크에 자세히 설명되어 있으니 추가 설명이 필요하다면 아래 링크를 참고하면 된다.
- 자기상관성(Autocorrelation): https://bing-su-b.tistory.com/133
[ SAS ] - 자기상관성(Autocorrelation)
지금까지 계속 회귀 분석을 하는 여러 프로그램을 살펴 봤다. 이번 실습 시간에도 작성한 프로그램에서 회귀 분석 시 발생할 수 있는 문제인, 자기상관성을 관찰해 볼 것이다. 프로그램을 작성
bing-su-b.tistory.com
- Durbin-Watson(DW) d Test: https://bing-su-b.tistory.com/134
[ SAS ] Durbin-Watson(DW) d Test
이전 게시물에서 오차항에 자기상관(autocorrelation)이 있는 경우에 대해 살펴봤다. 그와 더불어 오차항에 자기상관이 있는지 여부를 테스트하는 방법에 대해서는 추후 다룬다고 했는데, 이번 게시
bing-su-b.tistory.com
- Durbin's h Test: https://bing-su-b.tistory.com/135
[ SAS ] Durbin's h Test
이전 게시물에서 오차항(error term)이 자기상관을 가지는지 검정하는 방법인 Durbin-Watson(DW) d Test에 대해 다뤘다. 이때 이전 시점의 종속 변수가 현재 시점의 종속 변수에 영향을 미치는 회귀 모형
bing-su-b.tistory.com
(3-2)를 만족하지 못한다는 것은 인 경우로, 오차항(error term) 의 분산(variance)이 에 따라 다른 이분산(Heteroscedasticity)을 말하는 것이다. 이러한 상황은 아래와 같은 데이터 분포로부터 관찰할 수 있다.
- 이분산(Heteroscedasticity)이 존재하는 경우

이때 파란 직선이 회귀 직선이며, 빨간 별표는 실제 데이터 값이다. 해당 Data에서는 독립 변수 값이 증가할수록 오차항(error term)의 분산이 점차 커지는 패턴을 관찰할 수 있다. 즉, 오차항의 분산이 일정하지 않고 독립 변수 값이 커질수록 그 불확실성이 증가한다는 것이다.
- 공분산(Homoscedasticity)이 존재하는 경우

해당 Data에서는 독립 변수 값에 관계 없이 오차항(error term)의 분포가 회귀 직선 주변에 고르게 퍼져 있는 것을 관찰할 수 있다. 이를 통해 오차항의 분산이 일정하다는 결론을 내릴 수 있으며, 이는 회귀 분석에서 오차항의 등분산성 가정을 충족하는 것이다.
[ 이분산 검정법: White Test ]
회귀 모형의 오차항(error term)에 이분산이 존재하는지 검정하기 위하여 Halbert White가 제안한 White Test를 활용할 수 있다. 이분산 검정을 위한 기본 회귀 모형은 다음과 같이 2개의 독립 변수를 가지는 것을 가정한다.
이분산(Heteroscedasticity)은 오차항()의 분산이 t에 따라 다르다는 것이고, 보통 분산이 다를 경우 독립 변수에 영향을 받는 것이라고 판단하기 때문에 White Test는 다음과 같은 회귀 분석을 추가하여 검정을 진행한다.
①
위 식의 parameter 를 OLS 방식으로 추정하여 검정하고자 하는 귀무가설은 다음과 같다.
(오차항이 등분산성을 가진다는 의미)
해당 귀무가설을 다음과 같은 검정 통계량(test statistic)을 이용하여 검정한다.
- : 식 ①의 Sample 수
- : 회귀 모형 ①의 결정 계수(coefficient of determination)
- : 자유도(degrees of freedom of the test).
: 처음 가정한 회귀 모형의 절편을 포함한 parameter 개수
귀무가설을 기각한다는 것은 오차항 에 이분산이 존재하여 Classical assumption 3번의 2번째를 만족시키지 못한다는 결론을 내릴 수 있다. 반대로 귀무가설을 기각하지 않는다는 것은 오차항 이 등분산성을 가지며, OLS의 가정을 만족한다고 판단할 수 있는 것이다.
※ Lagrange Multiplier Test (LM Test)
Lagrange Multiplier 검정은 귀무가설을 유지하며 제약 조건이 통계적으로 유의한지 확인하는 방법이다. White Test에서는 이분산성 존재 여부를 검정하는 데 LM 검정 통계량(LM Test Statistic)을 이용하며, 이는 에 해당한다. 이 통계치는 구하기 쉬워 자주 이용되며 카이제곱 분포()를 따른다.
[ 이분산 검정법: Breusch-Pagan (Breusch) Test ]
Breusch-Pagan (Breusch) Test를 위한 기본 회귀 모형은 다음과 같이 가정한다.
여기서 이며, 오차항의 분산은 다음과 같이 가정한다.
이때 독립 변수 는 이분산성에 영향을 미치는 변수들이라고 생각하면 된다. 원래 회귀 모형의 변수들이거나 이들의 변형된 변수이다.
- Breusch-Pagan 검정 절차
- 기본 회귀 모형의 parameter들을 OLS 방식으로 추정하고, 잔차(residual) 를 구한다.
- 을 종속 변수로 설정하고, 다음 보조 회귀 모형을 OLS 방식으로 추정한다.
- Breusch test statistic 를 계산한다.
- 귀무가설 을 분포를 사용하여 검정한다.
※ White Test vs Breusch-Pagan Test
White Test는 비선형 및 상호작용 항까지 모두 포함하여 더 일반적인 이분산을 검정하는 반면, Breusch-Pagan Test는 선형 형태의 이분산을 검정하는 것이 차이다.
아래 링크는 이분산을 검정하기 위하여 의 p-값 계산을 할 수 있는 사이트이다.
링크: https://www.socscistatistics.com/pvalues/chidistribution.aspx#google_vignette
Quick P Value from Chi-Square Score Calculator
This calculator is designed to generate a p-value from a chi-square score. If you need to derive a chi-square score from raw data, you should use our chi-square calculator (which will additionally calculate the p-value for you). The calculator below should
www.socscistatistics.com
해당 사이트에 카이제곱 검정 통계량을 입력하면, 해당 값에 대한 p-값을 계산해주며 이를 통해 귀무가설의 기각 여부를 결정할 수 있다.
통계 개념에 대한 설명은 여기서 마무리를 하고, 프로그램 작성에 필요한 SAS 개념을 짚고 넘어가보려 한다. (이전 실습에서 다룬 개념은 다루지 않습니다. 이 게시물에서는 다루지 않는 개념이지만, 코드를 살펴보며 생소한 개념이 있으시다면 제 블로그 검색 or 이 카테고리에 있는 글을 읽고 와 주세요.)
[ White Test 수행 ]
White Test를 수행하기 위하여, Procedure MODEL 에서 WHITE Option을 사용할 수 있다. Procedure MODEL은 비선형 회귀 모형과 선형 회귀 모형을 모두 추정할 수 있는 명령어다. 해당 문법을 정리하면 아래와 같다.
- 명령어 정리
PROC MODEL DATA=xxx;
/* 종속 변수(Y)를 예측하기 위해 독립 변수(X)를 사용한 regression model 설정 */
MODEL Y=X / WHITE; /* White Test를 수행하기 위한 통계치 계산 Option(WHITE) 사용 */
RUN;[ Breusch-Pagan Test 수행 ]
Breusch-Pagan Test를 수행하기 위하여, Regression Procedure에서 BREUSCH Option을 사용할 수 있다. 해당 Option에서는 이분산에 영향을 줄 것으로 예상되는 독립 변수들 혹은 그들의 변형 형태를 명시해야 한다. 해당 문법을 정리하면 아래와 같다.
- 명령어 정리
PROC MODEL DATA=xxx;
/* 종속 변수(Y)를 예측하기 위해 독립 변수(X)를 사용한 regression model 설정 */
MODEL Y=X / BREUSCH=(Z1 Z2 ... Zp); /* Breusch Test를 위한 Option(BREUSCH) 사용 */
RUN;[ White Test와 Breusch-Pagan Test 함께 수행 ]
parameter를 PARMS 문을 통하여 명시적으로 선언하여 회귀 모형을 정의한 후 White Test와 Breusch-Pagan Test를 수행할 수 있다. 해당 문법을 정리하면 아래와 같다.
PROC MODEL DATA=xxx;
PARMS const beta1; /* 회귀식의 파라미터 선언 */
y = const + beta1 * x; /* 모형 정의 */
FIT y / WHITE BREUSCH = (Z1 Z2); /* White Test와 Breusch-Pagan Test 수행 */
RUN;
위의 개념들을 토대로 이제 실습을 진행해보려고 한다.
[ 이분산(Heteroscedasticity)을 검정하는 프로그램 ]
DATA ex;
seed1=1234;
seed2=5678;
int=10; /* 절편 설정(true value) */
alpha=0.1; /* 오차항의 분산을 조정하는 상수 */
beta=0.1; /* 기울기 설정(true value) */
DO i=1 TO 200;
x=i; /* 독립 변수 값 */
x2=x*x;
/* 이분산(Heteroscedasticity) error term 생성 */
sqx=SQRT(x); /* 이분산이 과도하게 증가하는 것을 방지하기 위함 */
sx=alpha*sqx;
u=sx*RANNOR(seed1);
y=int+beta*x+u; /* 종속 변수 값 */
OUTPUT; /* DO Loop 내부의 변수 값들을 모두 기억*/
END;
RUN;
/* regression 1 */
PROC REG DATA=ex;
MODEL y=x;
OUTPUT OUT=out1 P=pred R=resid;
/* regression 결과 Predicted(P)=pred로, Residual(R)=resid로
표기하여 이 변수들을 DATA 바구니 out1에 담는다. */
RUN;
DATA ex;
/* out1 DATA 바구니를 ex DATA 테이블에 담는다. */
SET out1;
resq = resid**2; /* 잔차 제곱을 resq로 저장 */
RUN;
/* plotting 1 */
PROC GPLOT DATA=ex;
PLOT resid*x; /* 세로축을 resid, 가로축을 x로 지정 */
SYMBOL V=STAR I=JOIN C=BLUE; /* Symbol Setting */
RUN;
/* plotting 2 */
PROC GPLOT DATA=ex;
PLOT pred*x y*x / OVERLAY; /* pred*x y*x 그림을 겹쳐 그림 (OVERLAY Option) */
SYMBOL1 V=DOT I=JOIN C=BLUE; /* pred*x에 사용되느 Symbol Setting */
SYMBOL2 V=STAR C=RED; /* y*x에 사용되는 Symbol Setting */
RUN;
/* regression 2 */
PROC REG DATA=ex;
MODEL resq=x x2;
RUN;
/* regression 3 */
PROC MODEL DATA=ex;
PARMS const beta1; /* 절편과 회귀 계수 설정 */
y=const+beta1*x; /* 기본 회귀 모형 */
FIT y / WHITE Breusch=(1 x x2); /* White Test와 Breusch-Pagan Test 수행 */
RUN;
이분산성을 가진 데이터를 생성하여 White Test와 Breusch-Pagan Test를 수행하는 프로그램이다. 해당 프로그램의 실행 결과를 나타내면 아래와 같다.

x의 parameter인 은 0.10241로 추정되었다.

다음의 plotting 결과로 이분산(Heteroscedasticity) 때문에 x 값이 증가하며 잔차(residual)의 분산(variance)이 증가함을 확인할 수 있다.
- 회귀 모형: 분석 결과

잔차 제곱을 종속 변수로 설정하여 회귀 모형을 설정하고 이 모형의 회귀 분석을 진행한 결과는 왼쪽과 같다. 도출된 n 값 200, R-Square 값 0.0975를 이용하여 White Test statistic을 계산하면 이다. 이는 오른쪽 결과에서 도출된 White Test의 statistic 값 19.50과 동일하다.
해당 통계량의 p Value는 앞서 소개한 사이트에 입력하여 다음과 같이 도출할 수 있다. 도출된 p Value는 0.000058임을 확인할 수 있다.
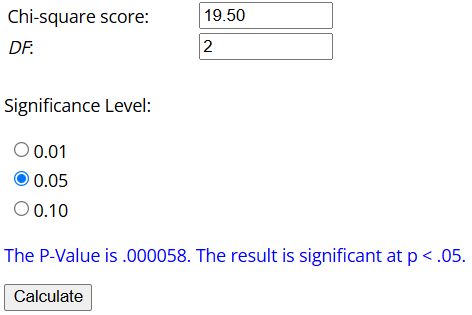
한편, White Test의 statistic 값은 선형 regression 결과를 이용하여 직접 계산할 수도 있지만, 귀무가설 기각 여부는 Chi-Square Table을 이용(아래 사이트 참고)하거나 p Value를 구해서 결정해야 한다.
- Chi-Square Table: https://people.richland.edu/james/lecture/m170/tbl-chi.html
Table: Chi-Square Probabilities
Table: Chi-Square Probabilities The areas given across the top are the areas to the right of the critical value. To look up an area on the left, subtract it from one, and then look it up (ie: 0.05 on the left is 0.95 on the right) df 0.995 0.99 0.975 0.95
people.richland.edu
기각 여부 결정 방법을 간단히 정리하면 다음과 같다.
- Chi-Square Table 이용
: 를 계산한 후 Chi-Square Table에서 유의수준()과 자유도()에 해당하는 임계값을 찾는다. 검정 통계량 가 임계값보다 큰 경우 귀무가설을 기각한다. - p Value 이용
: 검정 통계량 에 해당하는 p 값을 계산하여 귀무가설 기각 여부를 결정한다.
그러나 매번 검정 통계량 를 직접 계산하고 귀무가설을 기각할 지를 결정하기에는 불편함이 있기 때문에 SAS의 MODEL Procedure에서 제공하는 White Test와 Breusch-Pagan Test Option을 사용하는 것을 추천한다.
Procedure MODEL을 수행한 결과는 오른쪽과 같다. 해당 프로그램에서 White Test와 Breusch-Pagan Test를 위한 회귀 모형은 다음과 같이 설정하였다.
White Test와 Breusch-Pagan Test에서 독립 변수는 와 으로 설정되었기 때문에 자유도(DF)는 동일하게 2가 된다. 즉, 두 검정법에서 독립 변수의 구성과 자유도가 동일하기 때문에 Test Statisic 결과도 19.50으로 동일하게 나오는 것을 확인할 수 있다. Pr>ChiSq 값은 0.05보다 훨씬 작은 값이므로 두 Test 모두 등분산성(Homoscedasticity)을 가정하는 귀무가설을 강하게 기각한다.
[ 실제 데이터를 사용하여 Heteroscedasticity를 검정하는 프로그램 ]
DATA ip;
INFILE '/home/u63329964/mydata/ip.prn'; /* mydata 디렉토리의 ip.prn 파일을 불러옴 */
INPUT mon ip; /* mon, ip 변수에 데이터를 입력할 것임 */
logip=LOG(ip); /* ip 값에 자연 로그(ln)을 취함 */
/* ip의 성장률을 바꾸는 Logic */
ipg=DIF(logip)*1200; /* 연간 퍼센트 성장률 > 12*100=1200 */
ipg1=LAG(ipg); /* ipg 변수를 한 시점씩 밀어줌 */
RUN;
DATA fyff;
INFILE '/home/u63329964/mydata/fyff.prn'; /* mydata 디렉토리의 fyff.prn 파일을 불러옴 */
INPUT mon fyff; /* mon, fyff 변수에 데이터를 입력할 것임 */
fyff4=LAG4(fyff); /* fyff 변수를 한 시점씩 밀어줌 */
fyff4sq=fyff4*fyff4; /* fyff4 변수를 제곱 */
RUN;
DATA unemp;
INFILE '/home/u63329964/mydata/unemp.prn'; /* mydata 디렉토리의 unemp.prn 파일을 불러옴 */
INPUT mon unemp; /* mon, unemp 변수에 데이터를 입력할 것임 */
dunemp=DIF(unemp)*10; /* 월간 변화량에 10을 곱하여 조정 */
dunempsq=dunemp*dunemp; /* dunemp 변수를 제곱 */
RUN;
DATA all;
MERGE ip fyff unemp;
BY mon; /* mon 변수를 기준으로 병합 */
IF mon<19590101 OR mon>20191201 THEN DELETE;
num=__N__;
fydu = fyff4*dunemp; /* 두 독립 변수를 곱한 값 정의 */
RUN;
/* regression 1 */
PROC REG DATA=all;
MODEL ipg=fyff4 dunemp;
/* regression 결과 Residual(R)=resid로 표기하여
이를 DATA 바구니 out1에 담는다. */
OUTPUT OUT=out1 R=resid;
RUN;
DATA all;
/* out1 DATA 바구니를 all DATA 테이블에 담는다. */
SET out1;
resq=resid*resid; /* 잔차 제곱을 resq로 저장 */
RUN;
/* regression 2 */
PROC REG DATA=all;
/* White Test를 위한 회귀 모형 */
MODEL resq=fyff4 dunemp fyff4sq dunempsq fydu;
/* Breusch-Pagan Test를 위한 변수의 적합성 확인 */
MODEL resq=dunempsq fydu;
MODEL resq=dunempsq;
RUN;
/* regression 3 */
PROC MODEL DATA=all;
PARMS const beta1 beta2; /* 절편과 회귀 계수 설정 */
ipg=const + beta1*fyff4 + beta2*dunemp; /* 기본 회귀 모형 */
FIT ipg / WHITE BREUSCH=(1 dunempsq); /* White Test와 Breusch-Pagan Test 수행 */
RUN;
이분산(Heteroscadasticity) 검정을 실제 데이터에 적용하는 방법을 다루는 프로그램이다. 종속 변수를 ipg, 독립 변수를 fyff4, dunemp로 두고 분석하였으며, 기간은 1959년 1월부터 2019년 12월로 코로나 위기 기간을 제외하였다. (총 732개) 회귀 모형을 분석한 결과는 아래와 같다.
- 회귀 모형 1:
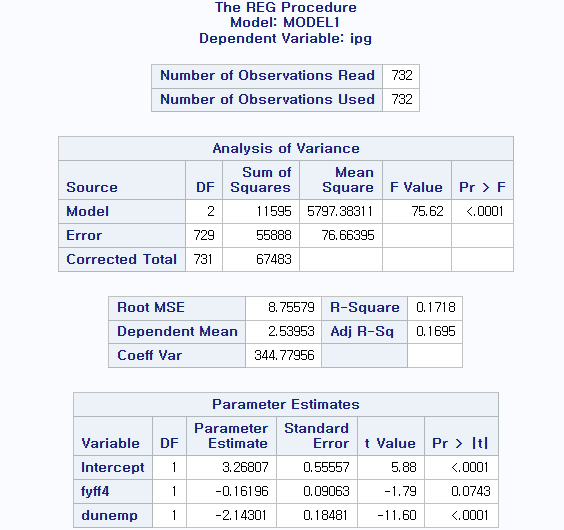
회귀 모형의 전반적인 적합도를 살펴보자. p value 값이 0.05보다 훨씬 작은 값이므로 독립 변수들이 종속 변수 를 설명하는 데 통계적으로 유의하다고 판단할 수 있다. 또한 R-Square 값은 0.1718로 독립 변수 와 가 종속 변수 의 변동을 약 17.18% 설명한다. R-Square 값이 다소 낮기 때문에, 이는 다른 변수들이 추가적으로 고려될 필요가 있다는 점을 시사한다. 해당 결과만으로는 OLS 추정치의 신뢰성이 다소 떨어진다고 볼 수 있다. 즉, 잔차에 대한 분석이 부족하기 때문에 자기상관성이나 이분산 등을 추가 검정하는 과정이 필요하다.
- White Test를 위한 regression 결과
White Test를 위한 회귀 모형(Regression Model)을 다음과 같이 설정하여 분석을 진행하였다.
해당 모형의 분석 결과는 아래와 같다.

이때 White Test statistic 로 계산할 수 있으며, 자유도(DF)는 5이므로 해당 사이트에서 도출한 p Value는 0.000757이 된다. p Value 값이 0.05보다 작기 때문에 등분산성(Homoscedasticity)을 가정하는 귀무가설을 기각할 수 있다.
또한 주목할 점은 3개의 독립 변수의 parameter 추정치가 음수임을 확인할 수 있다.
| Variable | Parameter Estimate | t Value |
| fyff4 | -0.99381 | -0.17 |
| dunemp | -8.44678 | -1.08 |
| fyff4sq | -0.03071 | -0.07 |
종속 변수 은 항상 0보다 큰 수이다. White Test가 독립 변수들, 각 독립 변수의 제곱, 독립 변수들의 cross product를 모두 독립 변수로 포함하도록 되어 있으나, 이 독립 변수들의 parameter 추정치가 음수로 나오는 경우에는 이론적인 문제를 발생시킬 수 있다. 따라서 모형의 적합성과 해석의 일관성 측면에서 위와 같이 parameter 추정치가 음수인 3개의 독립 변수들을 제외하고 양수인 추정치를 가지는 독립 변수만을 사용하는 것이 합리적이다.
- 이분산을 설명하는 주요 변수 파악
resq를 종속 변수로 하고 양수의 parameter 추정치를 가지는 독립 변수 dunempsq와 fydu를 사용하여 회귀 분석을 진행하였다. 해당 회귀 모형의 분석 결과는 다음과 같다.

두 독립 변수 모두 여전히 parameter의 추정치는 양수이므로 문제는 없다. 그러나 fydu의 경우 p Value가 매우 크기 때문에 통계적으로 유의하지 않으며, 등분산성(Homoscedasticity)을 만족한다는 귀무가설을 기각시킬 수 없다. 즉, 이분산성(Heteroscedasticity)을 설명하는 데 기여하지 못하므로 Breusch-Pagan Test에서 fydu는 제외하고 dunempsq만 사용하여 분석을 진행하는 것이 타당하다고 할 수 있다.
- 이분산을 설명하는 주요 변수와 잔차 제곱의 회귀 분석 결과
resq를 종속 변수로 하고 최종적으로 이분산에 영향을 준다고 판단이 되는 dunempsq를 독립 변수로 두어 회귀 분석을 진행하였다. 해당 회귀 모형의 분석 결과는 다음과 같다.

이때 White Test statistic 로 계산할 수 있으며, 자유도(DF)는 1이므로 해당 사이트에서 p Value를 도출하면 0.00001보다 작다는 결과가 나온다. 이는 0.05보다 훨씬 작은 수치이기 때문에 등분산성(Homoscedasticity)을 가정하는 귀무가설을 기각할 수 있다.
또한 앞서 소개한 사이트의 Chi-Square Table을 이용하여 , 일 때의 값을 찾으면 아래와 같이 3.841임을 알 수 있다.

도출된 검정 통계량 이므로 귀무가설은 여전히 기각된다.
- PROC REG & PROC MODEL 분석 결과 비교

현재 실습에서는 선형 추정을 하고 있기 때문에 PROC REG와 PROC MODEL의 분석 결과가 동일하게 나온다. 즉, 해당 분석 결과를 토대로 PROC MODEL은 비선형 회귀 추정이 가능하기에 더 유연한 명령어라고 할 수 있지만, 기본적인 회귀 분석 겨과는 PROC REG와 동일하다는 것을 알 수 있다.
'Language > SAS' 카테고리의 다른 글
| [ SAS ] 회귀 모형의 오차 검정 (2) | 2024.12.17 |
|---|---|
| [ SAS ] 비선형 회귀 모형의 추정 (0) | 2024.12.17 |
| [ SAS ] 실제 DATA를 사용하여 DW d Test+Durbin's h Test 진행하는 프로그램 작성 (1) | 2024.10.21 |
| [ SAS ] Durbin's h Test (0) | 2024.10.19 |
| [ SAS ] Durbin-Watson(DW) d Test (0) | 2024.10.16 |





댓글 영역