고정 헤더 영역
상세 컨텐츠
본문

저번 실습까지는 모르는 모수가 하나인 "평균 회귀 모형(Mean Regression Model)"에 대해 학습했다. 이번 실습 때는 모르는 모수가 2개인 "단순 회귀 모형(Simple Regression Model)"에 대해 학습하려고 한다. 본격적인 프로그램 작성 전, 필요한 통계 개념을 짚고 넘어가자. 평균 회귀 모형에 대한 설명이 필요하다면 이전 게시물(https://bing-su-b.fbtistory.com/107)을 보고 오면 된다. (볼 사람만 알아서 보시면 됨)
[ 회귀 분석(regression analysis)의 정의 ]
회귀 분석(regression analysis)은 독립 변수와 종속 변수 간의 함수 관계를 규명하는 통계적 방법이다.
독립 변수(independent variable)는 입력값이나 원인을 나타내며 설명 변수(explanatory variable)라고도 한다. 종속 변수(dependent variable)는 결과물이나 효과를 나타내며 반응 변수(response variable)라고도 한다. 독립 변수와 종속 변수는 (x1,y1)(x1,y1) 쌍으로 표현하고 독립 변수의 집합을 대문자 X, 종속 변수의 집합을 대문자 Y로 표시한다. 결국 회귀 분석은 독립 변수 X의 분포를 분석하여 종속 변수 Y의 값을 예측하는 것이라고 할 수 있다. 다른 말로는 다양하게 분포된 X가 존재할 때 Y의 분포에 대해 알아내는 것이다.
[ 단순 회귀 모형(Simple Regression Model) ]
단순 회귀 모형은 변수가 XiXi, YiYi만 존재하고 이 두 변수 사이의 선형적 관계를 표현한다. 이 관계를 식으로 표현하면 아래와 같이 표현할 수 있다.
Yi=α+βXi+uiYi=α+βXi+ui
- YiYi: i번째 측정된 종속 변수(반응 변수) Y의 값
- XiXi: i번째 독립 변수(설명 변수) X의 값
- uiui: i번째 측정된 Y의 오차항(error term)
- αα, ββ: 회귀 계수(αα는 절편 회귀 계수, ββ는 기울기 회귀 계수)
이 모형은 모집단을 전부 알고 있어야 매개 변수(parameter) αα, ββ 값을 알 수 있다. 하지만 우리는 모집단을 모르는 경우가 훨씬 많기 때문에 표본(sample)을 추출해서 모집단을 추측하게 된다. 즉, 단순 회귀 모형에서는 회귀 계수인 αα, ββ의 모수, 오차항의 분산 σ2σ2을 추정하게 된다.
매개 변수의 값을 추정하는 방법에는 최소자승법(Ordinary Least-Squares. OLS Method)이 있다. 이 방법을 사용하여 αα, ββ를 추정한 값이 각각 aa, bb라 하면 우리가 추정한 단순 회귀 모형은 아래와 같이 쓸 수 있다.
Yi=a+bXi+eiYi=a+bXi+ei
- aa: OLS로 추정한 αα 값
- bb: OLS로 추정한 ββ 값
- eiei: 잔차(residual). 표본(sample)로 추정한 회귀식과 실제 관측값의 차이
아래 그림은 OLS를 사용하여 추정한 단순 회귀 모형의 형태를 나타낸 그래프이다.

[ 최소자승법(OLS Method)로 추정치를 얻는 방법 ]
회귀 모델이 Yi=α+βXi+uiYi=α+βXi+ui와 같이 주어질 때, 오차항 제곱의 합은 아래와 같이 나타낼 수 있다.
min∑ni=1~ei2=min∑ni=1(Yi−˜a−˜bXi)2⋯①min∑ni=1˜ei2=min∑ni=1(Yi−˜a−˜bXi)2⋯①
지금은 목적 함수를 최소화(minimization) 하는 단계를 아직 달성하지 않은 상태이다. 따라서 목적 함수 최소화를 통하여 얻어지는 αα, ββ의 추정치인 aa, bb와 다르다는 의미에서 위의 식에서는 ˜a˜a, ˜b˜b로 임의의 αα, ββ 추정치를 표기하였다.
- First Normal Equation(첫번째 정규 방정식)
① 식을 ˜a˜a에 대해 편미분하고, 그 값이 0이 된다고 하면 아래와 같은 식을 도출할 수 있다.
−2∑ni=1(Yi−˜a−˜bXi)=0−2∑ni=1(Yi−˜a−˜bXi)=0
∑ni=1(Yi−a−bXi)=0∑ni=1(Yi−a−bXi)=0
위와 같이 도출된 식을 First Normal Equation(첫 번째 정규 방정식)이라고 한다. 이 정규 방정식과 이후 설명할 두 번째 정규 방정식이 0이 되는 αα, ββ 값을 각각 aa, bb라 할 수 있다. (∵ FOC를 만족함) 본격적으로 식을 살펴보기 전에 Normal Equation(정규 방정식)에 대해 설명하자면, 이는 선형 회귀 상에서 알지 못하는 값(parameter)을 예측하기 위한 통계학적 방법론이다.
이제 도출된 First Normal Equation이 의미하는 바에 대해 살펴보자.
- ∑ni=1(Yi−a−bXi)=∑ni=1ei=0∑ni=1(Yi−a−bXi)=∑ni=1ei=0: OLS로 얻은 잔차(Residual) eiei의 합은 0이 된다.
- ∑ni=1Yi−∑ni=1a−∑ni=1bXi=nˉY−na−nbˉX=0∑ni=1Yi−∑ni=1a−∑ni=1bXi=n¯Y−na−nb¯X=0이 되고, 이는 ˉY=a+bˉX¯Y=a+b¯X로 나타낼 수 있다. 즉, OLS로 얻은 직선은 YiYi 값의 평균 ˉY¯Y와 XiXi 값의 평균 ˉX¯X를 통과함을 알 수 있다.
- Second Normal Equation(두번째 정규 방정식)
이제 ① 식을 ˜b˜b에 대해 편미분하고, 그 값이 0이 된다고 하면 아래와 같은 식을 도출할 수 있다.
−2∑ni=1Xi(Yi−˜a−˜bXi)=0−2∑ni=1Xi(Yi−˜a−˜bXi)=0
∑ni=1Xi(Yi−a−bXi)=0∑ni=1Xi(Yi−a−bXi)=0
위와 같이 도출된 식을 Second Normal Equation(두 번째 정규 방정식)이라고 한다. 첫 번째 정규 방정식에서 설명한 바와 같이 두 정규 방정식이 0이 되는 αα, ββ 값을 aa, bb라 하고, 도출된 Second Normal Equation이 의미하는 바를 살펴보자.
- ∑ni=1Xi(Yi−a−bXi)=∑ni=1Xiei=0∑ni=1Xi(Yi−a−bXi)=∑ni=1Xiei=0: 독립 변수(설명 변수) XiXi 벡터와 잔차(residual) 벡터 eiei가 서로 수직(Orthogonal)이 된다는 의미. (벡터의 내적이 0이 된다고 해석)
- 두 정규 방정식을 연립하여 OLS 추정치 a, b 구하기
첫번째 정규 방정식으로부터 도출된 ˉY=a+bˉX¯Y=a+b¯X을 변형하면 a=ˉY−bˉXa=¯Y−b¯X라는 식이 도출된다. 이 식의 a 값을 두번째 정규 방정식에 대입하면 아래와 같이 정리된다.
∑ni=1Xi(Yi−ˉY+bˉX−bXi)∑ni=1Xi(Yi−¯Y+b¯X−bXi)
=∑ni=1XiYi−ˉY∑ni=1Xi+bˉX∑ni=1Xi−b∑ni=1X2i=0=∑ni=1XiYi−¯Y∑ni=1Xi+b¯X∑ni=1Xi−b∑ni=1X2i=0
이를 다시 정리하면 아래와 같은 결과가 도출된다.
b=∑ni=1XiYi−nˉXˉY∑ni=1X2i−nˉX2b=∑ni=1XiYi−n¯X¯Y∑ni=1X2i−n¯X2
=∑ni=1XiYi−2nˉXˉY+nˉXˉY∑ni=1X2i−2nˉX2+nˉX2=∑ni=1XiYi−2n¯X¯Y+n¯X¯Y∑ni=1X2i−2n¯X2+n¯X2
=∑ni=1XiYi−ˉY∑ni=1Xi−ˉX∑ni=1Yi+∑ni=1ˉXˉY∑ni=1X2i−2ˉX∑ni=1Xi+∑ni=1ˉX2=∑ni=1XiYi−¯Y∑ni=1Xi−¯X∑ni=1Yi+∑ni=1¯X¯Y∑ni=1X2i−2¯X∑ni=1Xi+∑ni=1¯X2
=∑ni=1(Xi−ˉX)(Yi−ˉY)∑ni=1(Xi−ˉX)2=∑ni=1(Xi−¯X)(Yi−¯Y)∑ni=1(Xi−¯X)2
=∑ni=1xiyi∑ni=1x2i=∑ni=1xiyi∑ni=1x2i
(단, xi=Xi−ˉXxi=Xi−¯X, yi=Yi−ˉYyi=Yi−¯Y, ˉX=1n∑ni=1Xi¯X=1n∑ni=1Xi, ˉY=1n∑ni=1Yi¯Y=1n∑ni=1Yi)
ββ의 OLS 추정치 bb를 구하고, 이 값을 다시 a=ˉY−bˉXa=¯Y−b¯X에 대입하면 αα의 OLS 추정치 aa를 구할 수 있게 된다. 단, 현재의 OLS 추정치 aa와 bb를 얻기 위하여 사용한 가정은 없다. 계량경제학 내용을 다룰 때 어떤 결과를 도출하기 위해 필요한 가정은 무엇이었는지를 기억하는 것은 매우 중요하다.
[ 결정 계수(R-Square) ]
R-Square은 회귀 분석의 성능 평가 척도 중 하나로, 결정 계수라고도 한다. 이는 독립 변수가 종속 변수를 얼마나 잘 설명하는지를 나타낸다. R-Squared는 0과 1 사이 값을 가진다. 예를 들어 결정 계수가 0.3(30%)라고 하면 독립 변수가 종속 변수의 30% 정도를 설명한다고 할 수 있다.
- 결정 계수(R-Square) 계산 방법
R2=ESSTSS=1−RSSTSSR2=ESSTSS=1−RSSTSS
- TSS(Total Sum of Squares): 총 제곱합=(관측값-표본 평균)의 제곱합=∑ni=1(Yi−ˉY)2=∑ni=1(Yi−¯Y)2
- MSS(Model Sum of Squares, Explained SS, ESS): 회귀 제곱합=(추정값-표본 평균)의 제곱합=∑ni=1(^Yi−ˉY)2=∑ni=1(^Yi−¯Y)2
- ESS(Error Sum of Squares, Residual SS, RSS): 잔차 제곱합=(관측값-추정값)의 제곱합=∑ni=1(Yi−^Yi)2=∑ni=1(Yi−^Yi)2
- TSS = MSS + ESS (유도할 예정.)
- 결정 계수(R-Square) 유도
위에서 OLS 방법으로 얻은 αα와 ββ의 추정치 aa, bb를 사용하여 추정한 회귀 모형을 표기하면 Yi=a+bXi+ei⋯①Yi=a+bXi+ei⋯①가 되고, 이는 ˉY=a+bˉX⋯②¯Y=a+b¯X⋯②(∵ 첫 번째 정규 방정식)의 꼴로 정리할 수 있었다.
① - ②: Yi−ˉY=b(Xi−ˉX)+eiYi−¯Y=b(Xi−¯X)+ei
yi=bxi+ei(∵yi=Yi−ˉY,xi=Xi−ˉX)yi=bxi+ei(∵yi=Yi−¯Y,xi=Xi−¯X)
y2i=b2x2i+e2i+2bxieiy2i=b2x2i+e2i+2bxiei (∵ 양 변을 제곱)
∑ni=1y2i=b2∑ni=1x2i+∑ni=1e2i+2b∑ni=1xiei⋯③∑ni=1y2i=b2∑ni=1x2i+∑ni=1e2i+2b∑ni=1xiei⋯③
③식 우변 마지막 항 다시 정리: 2b∑ni=1xiei=2b∑ni=1(Xi−ˉX)ei2b∑ni=1xiei=2b∑ni=1(Xi−¯X)ei
=2b∑ni=1Xiei−2bˉX∑ni=1ei=0−0=0=2b∑ni=1Xiei−2b¯X∑ni=1ei=0−0=0
(∵ Second Normal Equation: ∑ni=1Xiei=0∑ni=1Xiei=0
, First Normal Equation: ∑ni=1ei=0∑ni=1ei=0)
위의 ta③ 식에 대입하면 아래와 같은 결과를 얻을 수 있다.
∑ni=1y2i=b2∑ni=1x2i+∑ni=1e2i∑ni=1y2i=b2∑ni=1x2i+∑ni=1e2i(TSS=MSS+ESS)
따라서 결정 계수(R-Square)를 유도하면 아래와 같은 식이 도출된다.
R2=MSSTSS=b2∑ni=1x2i∑ni=1y2i=1−ESSTSS=1−∑ni=1e2i∑ni=1y2iR2=MSSTSS=b2∑ni=1x2i∑ni=1y2i=1−ESSTSS=1−∑ni=1e2i∑ni=1y2i
- 결정 계수(R-Square)의 특성
- 단순 회귀 모형은 | b | 값이 증가하면 결정 계수(R2R2) 값도 증가한다. (반대도 성립한다.)
- 일반 회귀 모형의 독립 변수(설명 변수)의 개수가 증가하면 결정 계수(R2R2) 값이 증가하거나 변하지 않는다. 즉, 독립 변수(설명 변수)의 개수가 증가하면 결정 계수R2R2는 감소하지 않는다. (∑ni=1e2i∑ni=1e2i 감소)
[ 수정된 결정 계수(Adjusted R-Square, ˉR2¯R2) ]
다변량 회귀 분석에서는 독립 변수(설명 변수)가 유의하든, 유의하지 않든 독립 변수(설명 변수)의 수가 많아질수록 결정 계수(R-Square)가 커진다. 이러한 결정 계수의 단점을 보완하기 위해 수정된 결정 계수가 필요하다.
¯R2=1−ESS/(n−k)TSS/(n−1)¯R2=1−ESS/(n−k)TSS/(n−1) (k: 모수(parameter)의 개수)
수정된 설정 계수는 독립변수가 증가하면 무조건 증가하는 결정 계수의 문제점을 방지한다. 즉, 모형에 적합하지 않은(회귀 모델 설명력에 기여하지 못하는) 변수가 투입되면 결정 계수가 증가하더라도 수정된 결정 계수는 감소하게 된다. 이는 일종의 패널티를 부여하는 것이라고 할 수 있다.
마찬가지로 R2R2와 ˉR2¯R2를 도출하기 위하여 필요한 가정은 없다.
[ OLS 방식의 타당성 ]
True Regression 식을 쓰면 Yi=α+βX+ui⋯①Yi=α+βX+ui⋯①이 되며, 회귀 직선은 항상 (ˉX,ˉY)(¯X,¯Y)를 지나므로 ① 식으로부터 ˉY=α+βˉX+ˉu⋯②¯Y=α+β¯X+¯u⋯②를 유도할 수 있다.
①-②: Yi−ˉY=β(Xi−ˉX)+(ui−ˉu)Yi−¯Y=β(Xi−¯X)+(ui−¯u), 즉, yi=βxi+(ui−ˉu)yi=βxi+(ui−¯u)
위의 식으로부터 도출된 yiyi를 OLS 추정치 b=∑ni=1xiyi∑ni=1x2ib=∑ni=1xiyi∑ni=1x2i에 대입하자.
b=∑ni=1xi(βxi+ui−ˉu)∑ni=1x2ib=∑ni=1xi(βxi+ui−¯u)∑ni=1x2i
=∑ni=1βx2i∑ni=1x2i+∑ni=1xiui∑ni=1x2i−∑ni=1xiˉu∑ni=1x2i=∑ni=1βx2i∑ni=1x2i+∑ni=1xiui∑ni=1x2i−∑ni=1xi¯u∑ni=1x2i
=β+∑ni=1xiui∑ni=1x2i(∵∀i,E(ui)=0)=β+∑ni=1xiui∑ni=1x2i(∵∀i,E(ui)=0)
즉, b=β+∑ni=1xiui∑ni=1x2i⋯③b=β+∑ni=1xiui∑ni=1x2i⋯③로 정리가 된다.
위의 ③ 식을 살펴보자. 모수(parameter) ββ의 추정치 bb는 모수(parameter) ββ에 독립 변수(설명 변수) xixi와 error uiui로 만들어진 어떠한 종류의 오류를 더한 값이다. 이 식으로부터 OLS 방식으로 true parameter ββ를 추정하는 것의 타당성을 알아보도록 하자.
③ 식의 우변에서 분모에 있는 항 ∑ni=1x2i∑ni=1x2i는 독립 변수(설명 변수) xi=(Xi−ˉX)xi=(Xi−¯X)를 제곱해서 n번 더한 것이다. 그러므로 이 분모 값은 표본의 크기 n이 증가하면 계속 증가한다. 따라서 n→∞일 때 분모도 무한대로 발산하게 된다. 이에 비해, 분자 ∑ni=1xiui∑ni=1xiui에서 error term uiui는 확률 변수로 그 값이 +와 -가 될 수 있기 때문에 xiuixiui의 합은 n→∞가 되더라도 분모만큼 증가하지는 않을 것이다. 따라서 ③ 식에서 표본의 크기 n이 계속 증가하면 ∑ni=1xiui∑ni=1x2i∑ni=1xiui∑ni=1x2i는 0으로 수렴하므로 결국 b=β가 된다. 결국 표본의 크기가 많을수록 OLS 추정치 b가 true parameter β로 수렴하게 되므로, OLS 방식으로 true parameter를 추정하는 것은 좋은 방법이라고 할 수 있다.
[ 고전적 가정(Classical Assumptions) ]
그렇다고 OLS 방식이 다른 방법보다 무조건 좋다는 것은 아니다. OLS 방식으로 얻은 추정치 b가 얼마나 좋은지, 그 Quality를 알아보기 위해서는 "고전적 가정(Classical Assumptions)"이라 하는 3개의 가정이 필요하다. 3개의 가정에 대해 간단하게 먼저 살펴보고, 이후 밑에서 자세히 하나씩 살펴보자.
- 독립 변수(설명 변수) Xi는 확률 변수가 아닌(non-random), 고정된 상수(fixed constants)이다.
- ∀i,E(ui)=0
- E(uiuj)=0(i≠j),E(uiuj)=σ2(i=j)
1. 독립 변수(설명 변수) Xi는 확률 변수가 아닌, 고정된 상수이다.
말 그대로 독립 변수(설명 변수)는 non-random, 즉, 확률 변수가 아니며 일반적인 상수(constant)로 취급한다는 것이다. 우리가 가정했던 true 선형 회귀 모형을 다시 살펴보자.
Yi=α+βXi+ui
이 true 모형에서 좌변의 종속 변수(반응 변수) Yi는 항상 random variable이다. 우변에서의 α와 β는 당연히 상수이고, 독립 변수(설명 변수) Xi가 상수라고 가정해도 error term인 ui는 항상 random variable이므로 종속 변수(반응 변수) Yi 역시 항상 random variable, 즉, 확률 변수가 된다.
예를 들어 위 회귀식의 종속 변수(반응 변수) Yi를 소비(consumption)라고 하고, 독립 변수(설명 변수) Xi를 소득(income)이라고 하면 소득이 fixed constant라고 해도 소비는 random variable이 된다. 사실 이러한 가정은 경제적 현실에는 맞지 않을 수도 있다. 그럼에도 불구하고, 우리가 사용하는 모든 DATA는 과거의 값들이기 때문에 이미 알려진 값이라고 생각할 수 있고, 이는 변하지 않는 값(fixed constant)라고 말할 수 있다. 따라서 독립 변수(설명 변수) Xi를 fixed constant라고 하는 것은 크게 잘못된 것은 아니라고 할 수 있다.
2. ∀i,E(ui)=0
이 가정은 수학적 편의를 위하여 세워졌기 때문에 그냥 당연하게 생각하면 된다. 만약 E(ui)≠0이라면 적절한 상수를 더하거나 빼서 0으로 만들면 된다.
3. E(uiuj)=0(i≠j),E(uiuj)=σ2(i=j)
이 가정은 매우 중요하지만, 대부분의 경제 관련 DATA들이 만족시키지 못하는 가정이기도 하다. 이 가정은 쉽게 말하자면 error term들끼리는 서로 상관성(correlation)이 없다는 것이다. 이를 i≠j일 때와 i=j일 때로 나누어 생각해 보자.
- i≠j일 때
error term 끼리는 상관성이 없기 때문에 ui는 상호독립적이라고 할 수 있다. 이전의 게시물에서 잠시 언급했지만, 두 확률 분포가 서로 독립인 경우에는 공분산(covariance)이 0이 된다. (공분산 관련 자세한 개념은 여기서 보세요.)
두 확률 분포 ui,uj의 공분산은 Cov(ui,uj)=E(uiuj)−E(ui)E(uj)=0로 나타낼 수 있다. 이때, CA 2에 의해 E(ui)=0이므로 Cov(ui,uj)=E(uiuj)−0=0이 되고, 결국 E(uiuj)=0임을 알 수 있다. 이를 통해 통계적으로 확률 변수 i≠j일 때, ui,uj가 상관성이 없다는 것을 E(uiuj)=0 꼴로 표현할 수 있다.
이는 많은 거시경제 데이터가 만족시키지 못하는 부분이기도 하다. 즉, error term 간에 상관성이 존재한다는 것이다. 일단 이렇게만 설명하고 이에 관해서는 나중에 자세히 설명하도록 하자.
- i=j일 때
i=j일 때는 ∀i,E(u2i)=σ2이다. 이는 ui의 분산(variance)이 i에 상관 없이 σ2으로 똑같다는 것이며, 등분산성(homogeneity)을 가진다고 할 수 있다.
[ 고전적 가정(Classical Assumptions)이 중요한 이유 ]
- 고전적 가정이 모두 만족되면 가우스-마르코프 정리(Gauss-Markov Theorem)이 성립한다. 즉, OLS 추정치 b는 Best Linear Unbiased Estimator(BLUE)가 된다. BLUE에 대해 간단히만 정리하면 선형(linear)이고 불편(Unbiased)인 추정치 중에서 가장 효율적인(Efficiency가 높은) 추정량을 말한다. 쉽게 말하면 최고의 선형 불편 추정량이라 할 수 있다.
- 최소자승법(OLS)를 이용하여 모수(parameter)를 추정하는 모든 컴퓨터 프로그램들은 주어진 회귀 모형이 고전적 가정(CA) 1, 2, 3 모두를 만족시킨다는 가정 하에 결과물(output)을 계산하고 제시한다.
2번에 대한 부연 설명을 하려고 한다. 고전적 가정이 만족되지 않으면 SAS 프로그램뿐만 아니라, 모든 프로그램들이 제공하는 OLS 추정치들 중 parameter에 관한 추정치만 제외하고, 표준 오차(Standard Error), t 값(t Value), P 값(Pr > | t |) 모두 틀린 값이 된다. 결국 이 값들은 실제로는 구할 수 없지만 고전적 가정(CA)이 만족된다고 가정하고 얻은 값이라고 할 수 있기 때문에 데이터 회귀 분석에서 고전적 가정은 매우 중요하다고 할 수 있다.
한편, 많은 거시경제 데이터는 고전적 가정(CA) 3을 만족시키지 못한다. 따라서 이러한 데이터를 사용한 회귀 모형의 경우 OLS 방법으로 분석하면 컴퓨터 분석 결과가 편향될 수 있어 잘못된 결론을 초래할 수 있을 것이다. 이러함에도 불구하고 여전히 고전적 가정이 중요한 이유는 고전적 가정이 OLS 추정치의 신뢰성과 정확성을 보장하기 위한 기준이 될 수 있기 때문이다. 즉, 가정이 충족되지 않는다면 어떤 문제가 발생할 수 있는지 예측할 수 있고, 대안을 선택할 수 있게 해 주기에 더 나은 역할을 한다는 것이다.
한편, 고전적 가정이 성립되지 않음으로써 생성되는 문제를 해결하는 방법에 대해서는 추후 자세히 다룰 예정이다.
[ 추정치 b의 분산(variance) ]
추정치 b의 분산(variance)은 중요하다. Gauss-Markov Theorem을 이해하기 위해서도 필요하고, 컴퓨터가 계산하는 표준 오차(Standard Error)를 이해하기 위해서도 필요하다. 우선 b의 분산(variance)은 아래와 같이 정의된다.
Var(b)=E[b−E(b)]2=E[b−β]2 (∵ CA 1&2 만족하면 E(b)=β)
또한, 우리는 앞서 b=β+∑ni=1xiui∑ni=1x2i임을 확인했다.
즉, Var(b)=E[b−β]2=E[∑ni=1xiui∑ni=1x2i]2이다.
이 식을 조금 더 수학적으로 풀어 써 보자.
Var(b)=E[∑ni=1xiui∑ni=1x2i]2
=1(∑ni=1x2i)2E[∑ni=1(x2iu2i+2∑n−1i=1∑nj>ixixjuiuj)]
=1(∑ni=1x2i)2[∑ni=1x2iE(u2i)+2∑n−1i=1∑nj>ixixjE(uiuj)]
=1(∑ni=1x2i)2[∑ni=1x2iσ2+0](∵CA3)
이를 정리하여 Var(b)의 결론 식을 도출하면 Var(b)=σ2∑ni=1x2i이다. 이를 통해,
- True Standard error of b=√σ2∑ni=1x2i
- Sample Standard error of b=√s2∑ni=1x2i임을 알 수 있다.
b의 Variance를 구하기 위하여 필요한 가정은 고전적 가정(Classical Assumption) 1, 2, 3이다.
[ 추정치 a의 분산(variance) ]
α(절편. intercept parameter)의 OLS 추정치인 a의 분산은 b의 분산만큼 중요하지는 않다. 그러나 SAS 프로그램에서 계산된 값이 어떻게 계산되었는지 알아본다는 의미에서 필요하다. 우선 a의 분산은 아래와 같이 정의할 수 있다.
Var(a)≡E[a−E(a)]2
위에서 CA 1, CA 2가 만족되면 E(a)=α 이다. 그러므로
Var(a)=E[a−α]2
이고, First Normal Equation에 의해 a=ˉY−bˉX 이므로 위 식 Var(a)는
Var(a)=E[ˉY−bˉX−α]2
=E[(α+βˉX+ˉu)−bˉX−α]2
=E[−(b−β)ˉX+ˉu]2
=E[(b−β)2ˉX2+ˉu2−2(b−β)ˉXˉu]
이다. 위 식 안의 세 개의 항 각각에 대하여 Expectation을 계산해야 한다. 순서대로 계산해보자.
① E(b−β)2ˉX2=Var(b)ˉX2=σ2ˉX2∑ni=1x2i
② E[ˉu2]=E[1n∑ni=1ui]2=1n2E[∑ni=1ui]2
=1n2E[∑ni=1u2i+2∑n−1i=1∑nj>iuiuj=1n2[nσ2]=σ2n
③−E[2(b−β)ˉXˉu]=−2ˉXE[∑ni=1xiui∑ni=1x2i1n∑nj=1uj]=−2nˉXσ2∑ni=1xi∑ni=1x2i=0
(∵∑ni=1xi=0)
따라서 Var(a)은 아래와 같이 도출된다.
Var(a)=①+②+③=(1n+ˉX∑ni=1x2i)σ2
이를 통해,
- True standard error of a=√[1n+ˉX2∑ni=1x2i]σ2
- Sample standard error of a=√[1n+ˉX2∑ni=1x2i]s2
Var(b)와 비교했을 때 ˉX2에 의해 Var(a)가 훨씬 더 큰 상황이 생길 수 있다.
추정치(Estimator)의 Variance는 Sample Data의 변화에 대하여 얼마나 민감하게 반응하는지의 척도이다. 즉, 추정치의 Variance가 크다는 것은 Sample Data가 변할 경우 Estimator 값도 크게 바뀔 수 있다는 것을 의미한다. True parameter 값을 쉽게 추정하기 위해서라도 Sample의 변화에 따라 Estimator가 크게 변하는 상황은 좋지 않다. 따라서 여러 Estimator 중 어떤 값이 좋을 지를 결정하고자 한다면, 각 Estimator의 Variance를 비교하면 된다.
[ SAS 프로그램에서 제공하는 통계치 정리 ]
- Estimators: 필요한 가정 없음
- Intercept a=ˉY−bˉX
- Slope b=∑ni=1xiyi∑ni=1x2i - Standard Error of b=√s2∑ni=1x2i
: 고전적 가정(Classical Assumption) 1, 2, 3 필요함 - t value=t(b)=b√s2∑ni=1x2i=bstandarderror(b)
: 고전적 가정(Classical Assumption) 1, 2, 3 + 정규분포 ui∼N(0,σ2) 필요함 - p value=Pr>|t|=Prob[|t|>|t(b)|]
: 고전적 가정(Classical Assumption) 1, 2, 3 + 정규분포 ui∼N(0,σ2) 필요함
[ Gauss-Markov Theorem ]
고전적 가정(Classical Assumption)이 성립한다면, OLS로 얻은 추정치는 linear(선형)이며 unbiased(불편된) 추정치 중에서 가장 좋은, 즉, 분산(variance)이 가장 작은 추정치가 된다는 것이다. 먼저 linear(선형)와 unbiased(불편된)가 무엇인지 살펴보자.
(1) Linearity(선형)
어떠한 추정치가 linear 하다는 것은 그 추정치에 대한 식이 종속 변수(반응 변수)인 Yi에 대해 선형(linear)이라는 것이다. 예를 들어 β의 추정치인 b에 대한 식을 살펴보자.
b=∑ni=1xiyi−nˉXˉY∑ni=1x2i−nˉX2
위의 식에서 OLS 추정치 b는 종속 변수(반응 변수) Yi의 선형 함수(Linear Function)인 것을 알 수 있다. 만약 우변에 Y2i이 있거나 Yi+1Yi와 같이 Yi와 관련된 비선형 식이 존재한다면 추정치 b는 Linear Estimator가 아니라고 할 수 있다.
(2) Unbiasedness(불편성)
어떠한 추정치, 예를 들어 b가 unbiasedness(불편성)를 가진다는 것은 E(b)=β라는 것이다. 위에서 살펴본 식 ③을 이용하여 이를 증명해 보자. ("OLS 방식의 타당성" 부분에 나온 식 말하는 겁니다!)
b=β+∑ni=1xiui∑ni=1x2i
E(b)=E(β+∑ni=1xiui∑ni=1x2i)
=β+E(∑ni=1xiui∑ni=1x2i) (∵ β: parameter이므로 random variable 아님)
=β+∑ni=1E(xiui)∑ni=1x2i=β+∑ni=1xiE(ui)∑ni=1x2i (∵ CA 1)
=β(∵ CA 2: E(ui)=0) 즉, E(b)=β이다.
즉, b가 unbiased 하다는 것은 여러 개 값으로 나온 b 값들의 평균을 구하고, 그 값들이 무한하다면 결국 그 평균은 parameter β 값이 된다는 것이다. 이러한 결론을 도출하기 위하여 사용된 가정은 Classical Assumption 1, 2임을 알 수 있다.
[ Gauss-Markov Theorem 증명 ]
모순법(Proof of contradiction)을 사용하여 고전적 가정을 만족하는 b가 가장 좋은 추정치(BLUE, Best Linear Unbiased Estimator)라는 것을 증명하려고 한다. 먼저 OLS 추정치 b보다 더 나은, 더 작은 분산을 가진 b∗라는 추정치가 존재한다고 가정하자. 이를 수식으로 나타내면 아래와 같다.
b∗=b+∑ni=1CiYi⇒b∗=Linear+Linear ··· ①
Ci는 기존 OLS 추정치보다 분산이 더 작은 추정치를 만들기 위한 임의의 상수 값이라고 생각하면 된다. b는 linear estimator이고, ∑ni=1CiYi 값은 종속 변수 Yi의 선형 결합이므로, 이들의 합인 b∗ 역시 선형성을 가진다고 할 수 있다. 이제 estimator b∗가 unbiased 되어 있다는 것을 보이자.
E(b∗)=E(b+∑ni=1CiYi)
=β+∑ni=1CiE(Yi)
=β+∑ni=1Ci[E(α+βXi+ui)]
=β+α∑ni=1Ci+β∑ni=1CiXi+∑ni=1CiE(ui)
=β+α∑ni=1Ci+β∑ni=1CiXi (∵ CA 1, CA 2)
위의 식을 통해 E(b∗)≠β임을 확인할 수 있다. 이때 b∗가 unbiased 이기 위해서는 아래의 두 가정이 필요하다.
- ∑ni=1Ci=0
- ∑ni=1CiXi=0
그런 다음, ① 식을 다시 살펴보자.
b∗=b+∑ni=1CiYi=b+∑ni=1Ci(α+βXi+ui)
=b+α∑ni=1Ci+βsumni=1CiXi+∑ni=1Ciui
=b+∑ni=1Ciui (∵ b∗가 unbiased 되기 위한 두 가정)
한편, 앞서 OLS 추정치 b=β+∑ni=1xiui∑ni=1x2i라는 식을 도출할 수 있었다. 이를 위의 식에 대입하면 아래와 같이 식이 정리된다.
b∗=β+∑ni=1xiui∑ni=1x2i+∑nj=1Cjuj
b∗−β=∑ni=1xiui∑ni=1x2i+∑nj=1Cjuj
E(b∗−β)2=E[∑ni=1xiui∑ni=1x2i+∑nj=1Cjuj]2
=E[∑ni=1xiui∑ni=1x2i]2+E[∑nj=1Cjuj]2+2E[∑ni=1xiui∑ni=1x2i∑ni=1Cjuj]
이 식에서 나오는 세 가지 항을 각각 ①, ②, ③ 항이라고 하자. 각각에 대해 살펴보면 아래와 같다.
① E[∑ni=1xiui∑ni=1x2i]2
=1[∑ni=1x2i]2E[∑ni=1x2iu2i]+2E[∑n−1i=1∑nj>ixixjuiuj]
=σ2∑ni=1x2i[∑ni=1x2i]2+0=σ2∑ni=1x2i (∵ CA 3, E(uiuj)=0 for i≠j)
여기서 CA 3가 성립하지 않는다면 첫번째 줄의 E[∑n−1i=1∑nj>ixixjuiuj]가 무엇인지 컴퓨터가 정확히 알아야 한다고 생각해볼 수 있다.
② E[∑nj=1Cjuj]
=∑nj=1C2jE(u2j)+2[∑n−1i=1∑nj>iCiCjE(uiuj)]
=σ2∑nj=1C2j+0 (∵ CA 3, E(uiuj)=0 for i≠j)
③ 2E[∑ni=1xiui∑ni=1x2i∑nj=1Cjuj]
=2σ2∑ni=1Cixi∑ni=1x2i=2σ2∑ni=1Ci(Xi−ˉX)∑ni=1x2i
=2σ2∑ni=1CiXi∑ni=1x2i−2σ2ˉX∑ni=1Ci∑ni=1x2i=0−0 (∵ ∑ni=1CiXi=0 & ∑ni=1Ci=0)
따라서 E(b∗−β)2=Var(b∗)=①+②+③=σ2∑ni=1x2i+σ2∑nj=1C2j+0
한편, E(b−β)2=Var(b)=σ2∑ni=1x2i이었다.
∴ Var(b)=σ2∑ni=1x2i<Var(b∗)=σ2∑ni=1x2i+σ2∑nj=1C2j (∵ C2j>0 for all j)
그러므로 Var(b∗)가 Var(b)보다 작다는 가정에 모순된다. 따라서 고전적 가정 3개가 모두 충족되면 OLS Estimator b는 linear(선형)이며 unbiased(불편된) 추정치 중에서 가장 좋은, 즉, 분산(variance)이 가장 작은 추정치가 된다.
통계 개념이 꽤 길었다. 이제 단순 회귀 모형을 분석하는 프로그램을 작성해야 하는데, 이전에 해당 프로그램 작성을 위해 필요한 SAS 개념을 짚고 넘어가자. (이전 실습에서 다룬 개념은 다루지 않습니다. 이 게시물에서는 다루지 않는 개념이지만, 코드를 살펴보며 생소한 개념이 있으시다면 제 블로그에서 검색 or 이 카테고리에 있는 글을 읽고 와 주세요.)
프로그램을 짤 때, 저번 실습 때 사용한 ip.prn 파일과 fyff.prn 파일을 활용할 것이다. 해당 파일을 다운로드하는 방법은 저번 게시글(https://bing-su-b.tistory.com/109)을 참고해 주세요.
[ 테이블 옆으로 붙이기(MERGE) ]
SAS에서 테이블을 다루면서 테이블끼리 조합을 해야 하는 경우가 있다. 기준이 되는 테이블 A와 B를 생성하는 방법은 이전 실습 때도 수없이 해봤기 때문에 (DATA A; 꼴로 테이블 생성) 이에 대해서는 넘어가도록 하겠다. 두 테이블을 생성한 후, 명령어를 사용하여 테이블을 붙이면 된다.
- 명령어 정리
MERGE XXX YYY; /* XXX와 YYY를 옆으로 결합 */[ DATA Step에서 ROW_NUMBER(행 번호) 만들기 ]
SAS의 DATA Step에서는 DATA를 한 줄씩 읽는다. 그리고 내부 변수 "_N_"에 DATA ~ RUN을 몇 번 실행했는지를 저장한다. 즉, 내부 변수 _N_은 대부분 현재 읽는 DATA File의 행 번호와 일치한다. 따라서 _N_을 이용하면 쉽게 전체 데이터에 대한 일련번호를 만들 수 있다.
- 예시 명령어
DATA XXX; /* 새로운 TABLE XXX를 생성 */
SET AAA; /* 기존 TABLE AAA를 불러 옴 */
ROW_NUMBER=_N_; /* 행 번호를 _N_에서 불러 옴 */
RUN;[ SAS에서의 그래프 작성(산포도, 산점도) ]
자료들을 그림으로 도식화하는 방법 중 하나가 산포도 혹은 산점도이다. 이를 SAS에서 PLOT이나 GPLOT을 이용하여 나타낼 수 있다. 먼저 PLOT에 대해 살펴보자.
- 명령어 정리(PLOT)
PROC PLOT DATA=xxx;
PLOT var1*var2; /* 세로축을 var1, 가로축을 var2로 지정 */
HAXIS a TO b BY c; /* 가로축을 a부터 b까지 c만큼 증분하여 표현 */
VAXIS p TO q BY r; /* 세로축을 p부터 q까지 r만큼 증분하여 표현 */
RUN;좀 더 많은 기능을 사용하기 위해서 PLOT 대신 GPLOT을 사용하는 게 편하다. GPLOT으로 출력된 결과는 하나의 이미지라 사진 저장 기능 등을 이용하여 외부로 쉽게 저장할 수 있지만, PLOT은 텍스트 형태로 출력되어 외부에서 사용하기가 GPLOT보다 번거롭다. (엑셀이나 pdf로 내보낼 수는 있지만, 모양이 그렇게 깔끔하지는 못함)
- 명령어 정리(GPLOT)
PROC GPLOT DATA=xxx;
PLOT var1*var2; /* 세로축을 var1, 가로축을 var2로 지정 */
HAXIS a TO b BY c; /* 가로축을 a부터 b까지 c만큼 증분하여 표현 */
VAXIS p TO q BY r; /* 세로축을 p부터 q까지 r만큼 증분하여 표현 */
RUN;- GRAPH에서 사용되는 옵션 정리
| SAS command | 설명 | |
| I = options | JOIN | 직선으로 연결 |
| NONE | 산점도 | |
| NEEDLE | 수평축과 점들을 바늘 모양으로 연결 | |
| SPLINE | SPLINE 법 | |
| V = symbol | 관측값을 나타낼 기호를 지정 (0-9, A-Z, 특수 부호의 이름) | |
| C = symbol-color | 점과 연결선의 색 지정 | |
| CI = line-color | 연결선의 색 지정 | |
| CV = value-color | 점의 색 지정 | |
| H = height | 출력 기호의 크기 지정(단위: pct, cm, in 등) | |
| L = line-type | 연결선의 종류 지정(1-46: 1은 실선, 2는 점선 등) | |
| WIDTH = width | 연결선의 굵기 지정(default = 1) | |
[ 단순 선형 회귀 분석하기(REG) ]
일단 독립 변수(설명 변수)가 하나인 단순 선형 회귀 모형에 대한 statement를 이용하여 회귀 계수를 추정하는 방법에 대해 알아보려고 한다. 이를 수행하는 Procedure가 REG이다.(REGression의 약자)
- 명령어 정리
PROC REG DATA=xxx;
MODEL Y=X; /* 종속 변수(Y)를 예측하기 위해 독립 변수(X)를 사용한 regression model 설정 */
/* SAS University Edition에서는 아래의 명령어를 지원하지 않음. */
PLOT Y*X; /* 종속 변수(Y)를 세로축, 독립 변수(X)를 가로축으로 지정하여
두 변수 간의 산점도를 그림. 회귀 직선을 시각적으로 보여줌. */
RUN;[ 가상 데이터를 단순 회귀 모형으로 분석하는 프로그램 ]
1. 독립 변수를 고정된 값으로 사용하는 경우 - Classical Assumption 만족
DATA fun;
seed=12;
alpha=1.0; /* 절편 설정(true value) */
beta=0.1; /* 기울기 설정(true value) */
DO i=1 TO 200;
x=i; /* 독립 변수 값 */
u=2*RANNOR(seed); /* 오차항. Var(u)=4 */
y=alpha+beta*x+u; /* 종속 변수 값 */
OUTPUT; /* DO Loop 내부의 변수 값들을 모두 기억 */
END;
RUN;
/* regression */
PROC REG DATA=fun;
MODEL y=x; /* regression model */
/* regression 결과 Predicted(P)=pred로, Residual(R)=resid로
표기하여 이 변수들을 DATA 바구니 out1에 담는다.*/
OUTPUT OUT=out1 P=pred R=resid;
RUN;
DATA fun;
/* out1 DATA 바구니를 fun DATA 테이블에 담는다. */
SET out1;
RUN;
/* plotting */
PROC GPLOT DATA=fun;
PLOT y*x; /* 세로축을 y, 가로축을 x로 지정*/
SYMBOL V=STAR I=JOIN C=BLUE; /* GRAPH Option Setting */
RUN;
/* plotting */
PROC GPLOT DATA=fun;
PLOT pred*x y*x/OVERLAY; /* pred*x y*x 그림을 겹쳐 그림(OVERLAY Option) */
SYMBOL1 V=DOT I=JOIN C=BLUE; /* pred*x에 사용하는 SYMBOL Setting */
SYMBOL2 V=STAR C=RED; /* y*x에 사용하는 SYMBOL Setting */
RUN;
QUIT; /* SAS Code 마지막에 PROC GPLOT을 하면 PLOT을 2번 함. 이를 방지하기 위해 QUIT 사용 */
가상의 단순 회귀 모형을 만들어 회귀 분석을 진행하는 프로그램이다. 이 프로그램을 실행한 결과를 살펴보자.

200개의 sample로 회귀 분석을 한 결과이다. R-Square 값은 0.9004로, 이는 독립 변수가 종속 변수의 90.04% 정도를 설명한다고 할 수 있다. 우리가 설정한 True Intercept(실제 절편 값)은 α=1.0이었고, 프로그램에서 계산된 OLS 추정치는 0.74076이다. 또한, 실제 기울기 값은 β=1이었고, 프로그램에서 계산된 OLS 추정치는 0.10213이다.
α의 OLS 추정치 a의 t 값은 2.65로 95% critical value인 1.98보다 크므로, 귀무가설 α0=0는 기각된다. 또한, β의 OLS 추정치 b의 t 값은 42.32, 즉, 95% critical value인 1.98보다 크므로 귀무가설 β0=0 역시 기각된다. a,b의 t Value를 계산하는 과정은 아래에 자세히 있으니 살펴보시면 됨.
- a의 t Value=a−α0√s2(1n+ˉx2∑ni=1x2i)=ParameterEstimateStandardError=0.740760.27974=2.65>1.98
- b의 t Value=b−β0√s2∑ni=1x2i=ParameterEstimateStandardError=0.102130.00241=42.32>1.98
Pr > | t |는 P value를 나타낸다.해당 값은 t 값이 α=0,β=0이라는 가정 하에 얻은 t 값보다 클 확률을 나타낸다. t 값은 모수(parameter) 추정치와 표준 오차(Standard Error) 사이의 비율을 나타낸다.
t 값이 클수록 모수(parameter) 추정치가 유의하다고 한다. 즉, 귀무가설 α0=0,β0=0가 강하게 기각된다. 해당 프로그램에서 분석된 t 값을 이용하여 α0=0,β0=0 귀무가설을 검증해보자. 일단 2.65와 42.32 모두 95% 신뢰 수준에서의 t 값 1.98에 비해 훨씬 크다. 따라서 해당 귀무가설은 기각되어야 한다.
P 값으로도 해당 귀무가설을 검증해보자. P > | t |는 귀무가설 α=0,β=0일 때 계산된 t 값이 2.65(42.32)보다 커질 확률이 0.0087(<0.0001)일 확률을 나타낸다. 즉, 95%의 신뢰 수준에서 P<0.05이므로 해당 귀무가설은 기각되어야 한다. 즉, t 값과 P 값은 우리에게 같은 결론을 말해주지만, 동일한 결론에 도달하기 위한 기준이 다르다. t 값은 그 값 자체로 우리에게 귀무가설을 검증하게 해 주는 반면, P 값은 확률 값으로 환산 되어 우리가 귀무가설을 검증하게 해 준다.
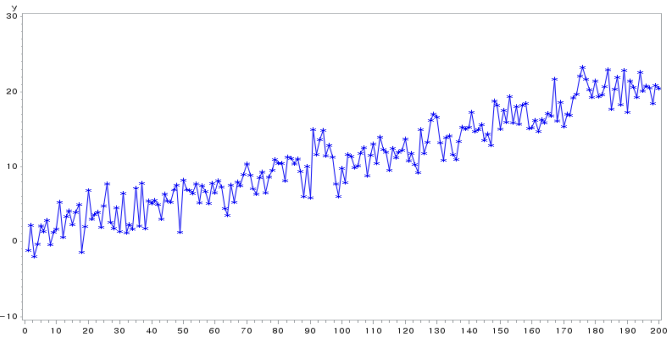
GPLOT을 통해 y와 x의 관계가 그림으로 도식화되어 나타나고 있다.
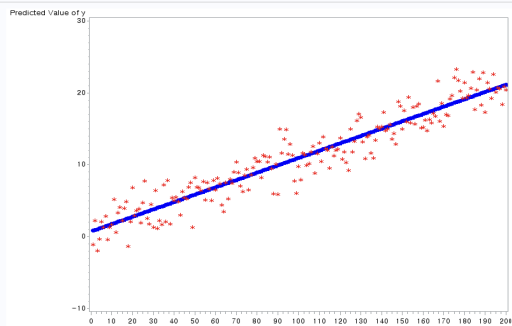
GPLOT을 통해 pred*x 관계를 도식화한 그림과 y*x 관계를 도식화한 그림을 겹쳐서 나타냈다.
2. 독립 변수에 무작위성(randomness)을 포함시키는 경우 - Classical Assumption 만족 X
DATA ex;
seed1 = 1234;
seed2 = 5678;
alpha = 10; /* 절편 설정(true value) */
beta = 0.1; /* 기울기 설정(true value) */
DO i=1 TO 200;
x = i + RANNOR(seed1); /* 무작위성이 부여된 독립 변수 값 */
u = 2*RANNOR(seed2); /* 오차항. Var(u)=4 */
y = alpha + beta*x + u; /* 종속 변수 값 */
OUTPUT; /* DO Loop 내부의 변수 값들을 모두 기억 */
END;
RUN;
/* plotting */
PROC GPLOT DATA=ex;
PLOT y*x; /* 세로축을 y, 가로축을 x로 지정 */
SYMBOL V=STAR I=JOIN C=BLACK; /* GRAPH Option Setting */
RUN;
/* regression */
PROC REG DATA=ex;
MODEL y=x; /* regression model */
/* regression 결과 Predicted(P)=pred로, Residual(R)=resid로
표기하여 이 변수들을 DATA 바구니 out1에 담는다. */
OUTPUT OUT=out1 P=pred;
RUN;
DATA ex;
SET out1;
RUN;
/* plotting */
PROC GPLOT DATA=ex;
PLOT pred*x y*x /OVERLAY; /* pred*x y*x 그림을 겹쳐 그림 (OVERLAY Option */
SYMBOL1 V=DOT I=JOIN C=BLUE; /* pred*x에 사용하는 SYMBOL Setting */
SYMBOL2 V=STAR C=RED; /* y*x에 사용하는 SYMBOL Setting */
RUN;
QUIT; /* SAS Code 마지막에 PROC GPLOT을 하면 PLOT을 2번 함. 이를 방지하기 위해 QUIT 사용 */
마찬가지로 위와 같이 가상의 단순 회귀 모형을 만들어 회귀 분석을 진행하는 프로그램이다. 그러나 이번 경우에는 독립 변수에 무작위성이 부여되었다. 이 프로그램을 실행한 결과를 살펴보자.
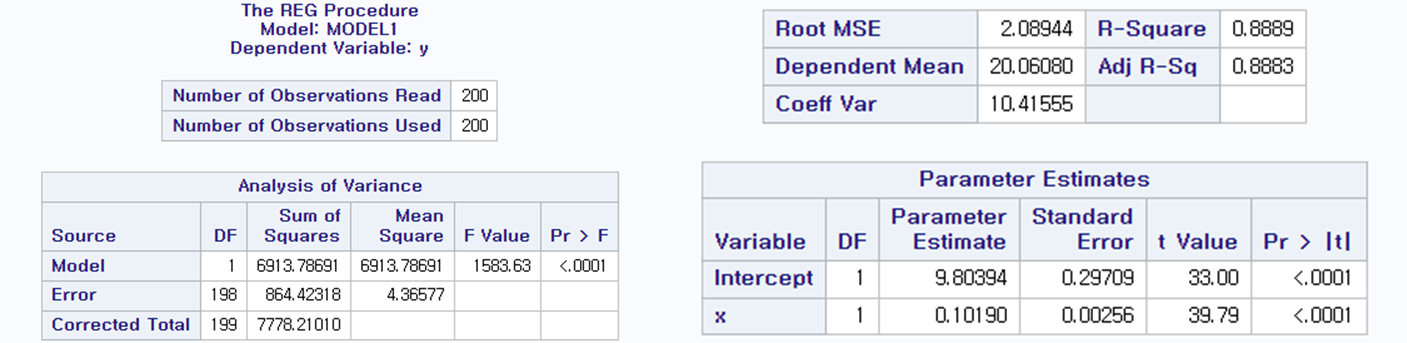
마찬가지로 200개의 sample로 회귀 분석을 한 결과이다. 주요 통계량을 살펴보면 아래와 같다.
- TSS(Total Sum of Squares) =∑ni=1y2i=7778.21
- MSS(Model Sum of Squares) =b2∑ni=1x2i=6913.79
- ESS(Error Sum of Squares) =∑ni=1e2i=864.42
- R-Squared =0.8889
- Adjusted R-Squared =1−ESS/(n−k)TSS/(n−1)=1−864.42/(200−2)7778.21/(200−1)=0.8883
우리가 설정한 True Intercept(실제 절편 값)은 α=10이었고, 프로그램에서 계산된 OLS 추정치는 9.80394이다. 또한, 실제 기울기 값은 β=0.1이었고, 프로그램에서 계산된 OLS 추정치는 0.10190이다.
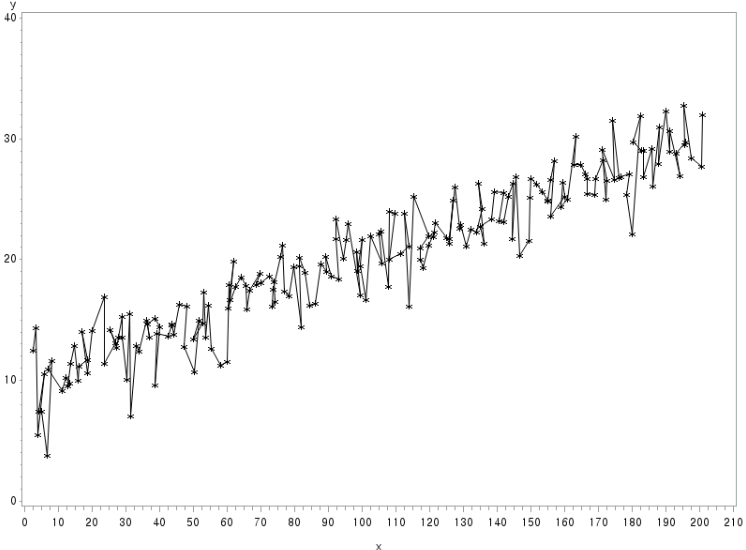
첫번째 GPLOT을 통해 y와 x의 관계가 그림으로 도식화되어 나타나고 있다.
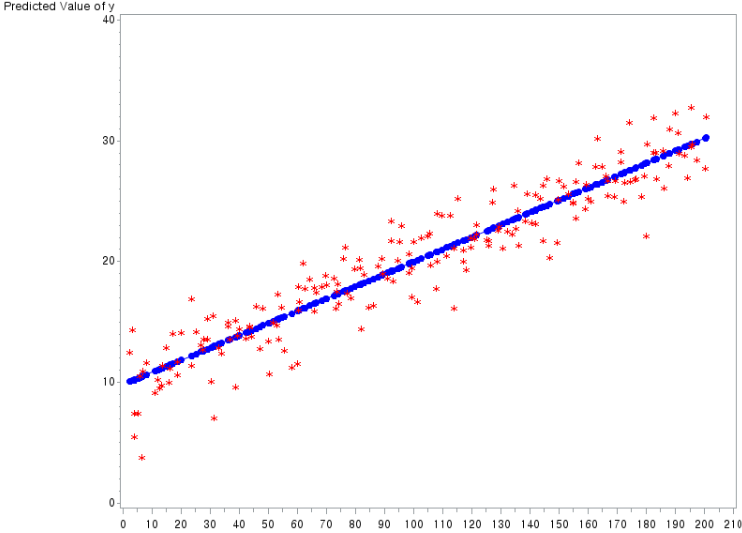
두번째 GPLOT을 통해 pred*x 관계를 도식화한 그림(회귀선)과 y*x 관계(종속변수 값)를 도식화한 그림을 겹쳐서 나타냈다.
나머지 실습 프로그램은 추후 게시물에 이어서 작성함. 링크: https://bing-su-b.tistory.com/111
[ SAS ] - 단순 회귀 모형을 분석하는 프로그램 작성 (2)
bing-su-b.tistory.com
'Language > SAS' 카테고리의 다른 글
| [ SAS ] - 다중공선성(Multicollinearity) (0) | 2023.06.16 |
|---|---|
| [ SAS ] - 단순 회귀 모형을 분석하는 프로그램 작성 (2) (0) | 2023.05.08 |
| [ SAS ] - 실제 Data를 사용한 평균 회귀 모형을 분석하는 프로그램 작성 + FRED site에서 실제 DATA FILE 다운로드 (0) | 2023.04.21 |
| [ SAS ] - 평균 회귀 모형에서 기초 통계량을 추출하는 프로그램 작성 + 가설 검정 (0) | 2023.04.21 |
| [ SAS ] - 정규 분포에서 기초 통계량을 추출하는 프로그램 작성 (0) | 2023.04.15 |





댓글 영역