[ SAS ] Durbin's h Test

이전 게시물에서 오차항(error term)이 자기상관을 가지는지 검정하는 방법인 Durbin-Watson(DW) d Test에 대해 다뤘다. 이때 이전 시점의 종속 변수가 현재 시점의 종속 변수에 영향을 미치는 회귀 모형은 DW d Test를 적용할 수 없다는 내용을 다뤘다. 이번 게시물에서는 이러한 상황을 해결할 수 있는 Durbin's h Test에 대해 다뤄보려고 한다. 실습을 진행하기 이전에 프로그램 분석에 필요한 통계적 개념을 짚고 넘어가자.

※ Durbin-Watson(DW) d Test를 수행하기 위한 가정 (복습)

DW d Test를 사용하기 위하여 충족되어야 하는 가정은 아래와 같다.

• 회귀계수(regressor)가 non-random하며 fixed인 상수(constant)여야 한다.
• 오차항(error term)은 AR(1) model에 따라 움직여야 한다. ($u_t=\alpha u_{t-1}+\varepsilon_t$)

아래와 같이 종속 변수의 시차항(lagged dependent variable)이 회귀 변수로 포함된 경우에는 첫 번째 가정을 위반하기 때문에 $u_t$에 대하여 DW d Test를 사용할 수 없다.

$Y_t=\beta_1+\beta_2 X_t+\beta_3 Y_{t-1}+u_t$

실제로 시차가 존재하는 종속 변수(lagged dependent variable)와 양의 자기상관을 가진 오차항(positively autocorrelated error term)이 결합된 경우에는 DW d Test를 하게 되면 통계량(statistic)이 실제 값보다 크게 계산될 수 있다. 이러한 결과 해석은 추후 실습에서 진행할 예정이다.

[ Durbin's h Test ]

Durbin은 DW d Test가 적용되지 않을 때 사용할 수 있는 h Test를 제시했다. h Test의 절차는 아래와 같다.

1. 아래의 회귀 모형에서 paramter들을 OLS 방식으로 추정한 후, 그에 따른 잔차 $e_t$를 구한다.
   $Y_t=\beta_1+\beta_2 X_t+\beta_3 Y_{t-1}+u_t$
   $u_t=\alpha u_{t-1}+\varepsilon_t$
2. 위에서 얻은 잔차 $e_t$를 사용하여 아래와 같은 회귀 모형의 parameter들을 OLS 방식으로 추정한다.
   $e_t=\gamma_0+\gamma_1 e_{t-1}+\gamma_2 Y_{t-1}+\nu_t$
3. 귀무가설 $\gamma_1=0$에 대한 t Test를 수행하여 오차항 $u_t$에 자기상관이 존재하는지 여부를 확인한다. 만약 귀무가설 $\gamma_1=0$이 기각되면 회귀 모형의 오차항 $u_t$에 자기상관이 없다는 귀무가설은 기각된다. $\gamma_1=0$이 기각될 수 없다면 $u_t$에 자기상관이 없다는 귀무가설도 기각될 수 없다.

위와 같이 진행되는 Durbin's h Test는 OLS 방식으로 regression을 두 번 실행하면 결과를 쉽게 얻을 수 있고, 충분히 익숙한 t Test를 활용하기 때문에 자기상관 여부를 쉽게 판단할 수 있다는 장점을 가진다.

- h 통계량(statistic) 계산

$Y_t=\beta_1+\beta_2 X_t+\beta_3 Y_{t-1}+u_t$

$u_t=\alpha u_{t-1}+\varepsilon_t$

위와 같은 회귀 모형에서 Durbin's h Test의 통계량 $h$는 아래와 같이 계산될 수 있으며, 이는 점근적으로 표준정규분포를 따른다. (asymptotic standard normal distribution) 따라서 Durbin's h Test에서 h 통계량을 계산한 후, 이 값을 표준 정규분포의 적절한 임계치(critical value)와 비교하여 귀무가설 기각 여부를 판단할 수 있다.

$h=\hat{\alpha} \sqrt{\frac{n}{1-n Var(b_3)}}$ ($\hat{\alpha}=\frac{\sum_{t=2}^n e_t e_{t-1}}{\sum_{t=1}^n e_t^2}$,  $b_3$: $\beta_3$의 OLS 추정치)

위 식으로부터 $n Var(b_3)>1$인 경우에는 h 통계량이 존재하지 않기 때문에 Durbin's h Test를 사용할 수 없다는 것을 알 수 있다. 

 

이제 이러한 개념을 종합하여 실습을 진행해보려고 한다. 코딩에 필요한 개념은 이전 게시물들에서 충분히 다루었기 때문에 생략한다. (개념 필요하신 분은 제 블로그에서 검색 or 해당 카테고리에서 찾아서 보시면 됨.)

[ Durbin's h Test를 수행하는 프로그램 ]

DATA ex;
	seed1=1234;
	seed2=5678;
	seed3=9012;
	
	alpha=0.7;  /* 오차항의 자기상관 계수 설정 */
	beta1=10;  /* 절편 설정 (true value) */
	beta2=0.1;  /* 기울기 설정 (true value) */
	beta3=0.3;  /* 종속 변수의 자기상관 계수 설정 */
	ulag=RANNOR(seed1);  /* 오차항 생성 */
	ylag=RANNOR(seed2);  /* 종속 변수 생성 */
	
	DO i=1 TO 200;
		x=i;  /* 독립 변수 값 */
		u=alpha*ulag+RANNOR(seed3);  /* 오차항끼리 자기상관관계 존재 */
		y=beta1+beta2*x+beta3*ylag+u;  /* 이전 시차의 종속 변수 포함된 회귀 모형 */
		OUTPUT;  /* DO Loop 내부 변수 값들을 모두 기억 */
		ulag=u;  /* 오차항을 이전 오차항으로 갱신 */
		ylag=y;  /* 종속 변수 값 이전 값으로 갱신 */
	END;
RUN;
/* regression 1: residual estiamte */
PROC REG DATA=ex;
	MODEL y=x ylag /DWPROB;  /* DWPROB Option을 활용하여 DW Test 진행 */
    /* regression 결과 Residual(R)=reisd로 표기하여
    이를 DATA 바구니 out1에 담는다. */
	OUTPUT OUT=out1 R=resid;
RUN;

DATA ex;
	/* out1 DATA 바구니를 ex DATA 테이블에 담는다. */
	SET out1;
	resid1=LAG(resid);  /* residual을 한 시점씩 밀어줌 */
RUN;
/* regression 2 */
PROC REG DATA=ex;
	/* regression model */
	MODEL resid=resid1 x ylag;
RUN;

 

해당 프로그램은 DW d Test에서 다뤘던 회귀 모형에서 종속 변수 $Y_{t-1}$을 추가하여 작성한 것이다. 종속 변수에 시차가 존재하기 때문에 DW d Test를 수행할 수 없으며 Durbin's h Test를 수행해야 하기 때문에 회귀 모형을 두 개를 세워서 분석해야 한다는 점을 반영하여 프로그램을 작성했다. 각각의 회귀 모델을 분석한 결과는 아래와 같다.

- 첫 번째 회귀 모형: $Y_t=\beta_1+\beta_2 X_t+\beta_3 Y_{t-1}+u_t$

첫번째 회귀모형 분석 결과

앞서 설명한 바와 같이 해당 모형은 종속 변수에 시차가 존재하기 때문에 DW d Test를 수행할 수 없다. 그럼에도 수행한 이유는 프로그램을 작성하며 오차항(error term)에 자기상관 계수 $\alpha$를 설정하였으므로, DW d Test를 하더라도 귀무가설 $\alpha=0$이 기각되는지를 살펴보기 위해서다. 

DW d Test 결과

설명한 김에 DW d Test 결과부터 살펴보자. 1st Order Autocorrelation 값은 0.310으로, 양의 상관관계가 존재함을 확인할 수 있다. 따라서 $pr<DW$ 값을 살펴볼 수 있고, 이 값이 0.001보다 작기 때문에 귀무가설 $\alpha=0$을 기각할 수 있다는 결론을 내릴 수 있다. 이를 통해 오차항 간에는 양의 자기상관이 존재함을 알 수 있다. 즉, 해당 실습에서 사용한 회귀 모형은 Durbin's h Test를 해야 함에도 DW d Test를 수행했을 때 귀무가설을 기각할 수 있을 만큼 강한 상관관계를 가진 모형이라고 해석할 수 있다.

Regression 결과

첫번째 모형의 parameter 추정 결과를 true value와 비교해보자. 설정된 true model은 아래와 같다.

$Y_t=10+0.1 X_t+0.3Y_{t-1}+u_t$

$u_t=0.7 u_{t-1}+\varepsilon_t$

이를 토대로 true value와 estimated value를 비교하면 아래와 같다.

	true value	estimated value
Intercept	10	3.95192
$\beta_2$ ($X_t$'s parameter)	0.1	0.03917
$\beta_3$ ($Y_{t-1}$'s parameter)	0.3	0.73274

표에서 관찰할 수 있듯이 추정치들은 true 값과 상당한 차이를 보인다. 이유는 오차항(error term)에 존재하는 자기상관 때문이다.

- 두 번째 회귀 모형: $e_t=\gamma_0+\gamma_1 e_{t-1}+\gamma_2 Y_{t-1}+\nu_t$

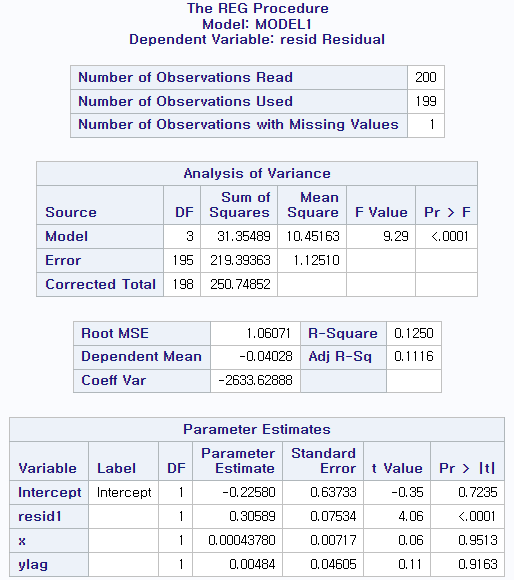
resid1의 parameter 추정치는 0.30589로 true 값인 0.7과는 상당히 차이가 있다. 이러한 차이는 종속 변수 간의 시차 때문에 발생한다고 추측할 수 있다. 이러한 결과로 오차항(error term)에 자기상관(autocorrelation)이 존재할 때, residual과 종속 변수의 과거 값들 간에 상관관계가 존재할 수 있어서 서로 추정치에 영향을 미친다는 사실을 알 수 있다. 

 

또한 resid1 paramter의 추정치에 대한 t Value는 4.06으로 1.98보다 훨씬 큰 값이며, P Value 역시 0.05보다 훨씬 작은 값이기 때문에 귀무가설 $\alpha=0$을 기각할 수 있다. 즉, Durbin's h Test를 통하여 오차항(error term)에는 자기상관이 존재한다는 결론을 내릴 수 있다.

 

이번 실습까지는 가상의 Data를 이용하여 생성된 회귀 모형을 분석했다. 다음 실습에서는 실제 Data를 이용하여 DW d Test와 Durbin's h Test를 하는 실습을 진행해보려 한다.