[ SAS ] - 정규 분포에서 기초 통계량을 추출하는 프로그램 작성

네 번째 실습으로는 정규 분포에서 기초 통계량(평균, 표준편차, 분산 등)을 추출하는 프로그램을 작성해 봤다. 이전의 게시물에서와 마찬가지로 프로그램 작성을 위하여 필요한 통계 개념을 먼저 짚고 넘어가려고 한다.

[ 정규 분포(Normal Distribution) ]

앞서 배웠던 이산 확률 분포는 셀 수 있거나 유한개의 값을 가진다. 그런데 무수히 많은 실수의 분포를 대상으로 할 경우도 존재하는데, 이런 식으로 확률 변수 X가 어떤 범위의 모든 실수 값을 가질 수 있을 때 이를 연속 확률 변수라고 표현한다. 이러한 연속 사건에서 x가 주어졌을 때의 확률을 구하는 함수를 확률 밀도 함수(PDF, Probability Density Function)라고 한다.

 

정규 분포 역시 대표적인 연속 확률 분포의 예시다. 정규 분포의 PDF는 아래와 같다.

$$f(x)= \frac{1}{ \sqrt{2 \pi  \sigma ^2} } e^{- \frac{1}{2 \sigma ^2}(x- μ)^2} $$

• $ \sigma ^{2} =Var(X)$:  true variance
• $μ=E(X)$: true mean. 모평균(모집단의 평균)
• $x$: 관측값. 즉, 확률 변수 X 값이 나타내는 값.

정규 분포에서의 정의역은 모든 실수기 때문에 $\int_{-\infty} ^ \infty  f(x)dx=1$이 된다.

 

정규 분포 곡선은 아래와 같은 특징을 가진다.

1. 종 모양의 그래프 개형을 가진다. 여기서 종 모양이란, 중심에 많은 데이터들이 모여 있고 중심에서 멀어질수록 적은 데이터를 포함하는 것을 말한다. 또한 중심을 기준으로 좌우 대칭적인 형태를 가지고 있다.
2. 평균 $μ$는 분포의 위치(location)을 나타내고, 퍼져 있는 정도(spread, 산포도)는 분산 $ \sigma ^{2} $에 의해 결정된다.
3. 어떠한 값이 평균 $μ$에서 표준편차 $k \sigma $(k: 자연수) 내에 있을 확률은 평균 $μ$ 및 분산 $\sigma^2 $에 관계없이 동일하다. (Empirical Rule)

$$Prob[\bar{X}-1 \sigma <μ<\bar{X}+1 \sigma ]=0.683$$

$$Prob[\bar{X}-1.96 \sigma <μ<\bar{X}+1.96 \sigma ]=0.950$$

$$Prob[\bar{X}-2 \sigma <μ<\bar{X}+2 \sigma ]=0.954$$

$$Prob[\bar{X}-3 \sigma <μ<\bar{X}+3 \sigma ]=0.997$$

- 정규 분포를 쓰면 좋은 통계적 상황

1. 정규 분포는 많은 모집단에 대해 상당히 좋은 근사치가 된다.
2. 표본 평균의 확률 분포는 분포 크기가 증가함에 따라 정규 분포에 근접한다. (중심 극한 정리, CLT)

아래의 설명은 중심 극한 정리에 관한 내용이다. 보실 분들만 참고해서 보시면 됩니다 :)

모집단이 평균이 μ이고 표준편차가 σ인 어떠한 분포를 따른다고 하자. 이때, 모집단에서 표본을 n만큼 뽑는다면, 표본 평균은 통계량이므로 어떠한 분포를 따르게 될 것이다. 이때, 모집단으로부터 추출된 '표본의 크기(표분의 수)가 충분히 크다면(일반적으로 n≥30)' 표본 평균들이 이루는 분포는 '평균이 $μ$이고 표준편차가 $ \frac{ \sigma }{ \sqrt{n} } $인 정규분포'에 근사한다.

평균과 분산에 따른 정규 분포 곡선 형태

.

[ 표준 정규 분포(Standard Normal Distribution) ]

평균이 $μ$이고 분산이 $ \sigma ^{2} $인 정규 분포는 $X \sim N( \mu , \sigma ^{2} )$의 형태로 표시된다.

 

정규 분포의 중요한 특징 중 하나는 정규 분포를 따르는 확률 변수의 선형 조합도 정규 분포를 따른다는 것이다. 예를 들어 평균이 10인 정규 분포를 따르는 데이터에 모두 -10씩을 해 주면 그들 역시 정규 분포를 따르고 평균은 0이 될 것이다. 같은 식으로 분산이 100인 정규 분포를 따르는 데이터에 모두 10씩 나누어주면 그들 역시 정규 분포를 따르고 분산은 1이 된다. 이는 곧 정규 분포는 중심과 scale을 자유자재로 바꾸어 줄 수 있는 유연성을 가졌다는 것이다.

 

이러한 성질을 이용해 각 데이터에서 평균을 빼고 표준편차를 나누어 주면 어떤 정규 확률 변수든 간에 평균이 0, 분산이 1인 동일한 단위를 갖게 된다. 이렇게 정규화된 분포를 표준 정규 분포(standard normal distribution)라고 한다.

$Y \sim N( \mu , \sigma ^{2}) $일 때, $( \frac{Y- \mu }{ \sigma } ) \sim N(0,1)$

$$E(Z)=E( \frac{X- \mu }{ \sigma } )= \frac{E(X)- \mu }{ \sigma } = \frac{ \mu - \mu }{ \sigma } =0$$

$$Var(Z)=E[Z-E(Z)]^2=E[Z-0]^2$$

$$=E[Z]^2=E[ \frac{X- \mu }{ \sigma } ]^2= \frac{1}{ \sigma ^2}E(x- \mu )^2 $$

$$=\frac{1}{ \sigma^2 }Var(X)= \frac{1}{ \sigma ^2}  \sigma ^2=1 $$

 

여기서도 위의 정규 분포에서 설명했던 Empirical Rule이 성립한다.

$$Prob[-1.65<Z<1.65]=0.90$$

$$Prob[-1.96<Z<1.96]=0.95$$

$$Prob[-2.58<Z<2.58]=0.99$$

[ 평균 회귀 모형(The Mean Regression Model) ]

확률 변수 $X_{i} $가 아래와 같은 식을 따른다고 가정하자.

$$X_{i}= \mu + \varepsilon _{i} $$

• $\mu $: 일정한 상수 값
• $ \varepsilon _{i} $: 평균이 0이고 분산이 $\sigma^2 $인 정규 분포 랜덤 변수다

이를 평균 회귀모형(mean regression model)이라 하자. $X_{i} $는 아래와 같은 분포를 가진다.

$$X_{i} \sim N( \mu ,  \sigma ^{2}) $$

• 정규 분포의 매개변수(parameter) $\mu $와 $\sigma ^2$은 각각 true mean, true variance다. 이 두 값은 알 수 없다.
• $i≠j$이면 $E( \varepsilon _{i} \varepsilon _{j})=0 $: $ \varepsilon _{i}$는 상호독립적이다.

위의 상호독립이라는 개념과 관련된 설명을 잠깐 해 보려고 한다.

두 확률 분포가 서로 독립인 경우에는 공분산(covariance)이 0이다. (공분산 관련 개념은 여기서 자세히 보세요.)

두 확률 분포 X, Y의 공분산은 $Cov(X, Y)=E(XY)-E(X)E(Y)$와 같이 나타낼 수 있다. 다시 말해, $ \varepsilon _{i}, \varepsilon_j$의 공분산은 $Cov( \varepsilon_i,  \varepsilon_j)=E( \varepsilon_i  \varepsilon_j )-E( \varepsilon_i)E( \varepsilon_j)$가 된다. 이때, 확률 변수 $\varepsilon _{i}$의 평균은 0, 즉, $E(\varepsilon _{i})=0$이므로 $Cov( \varepsilon_i,  \varepsilon_j)=E( \varepsilon_i  \varepsilon_j )-0=0$가 된다. 이는 결국 $E( \varepsilon_i  \varepsilon_j )=0$임을 의미한다.

따라서 $i≠j$이면 $E( \varepsilon _{i} \varepsilon _{j})=0 $: $ \varepsilon _{i}$는 상호독립적이다는 설명이 성립한다.

 

우리가 이 모형으로부터 추정하고 싶은 값은 현재 알 수 없는 true mean 값인 $\mu $이다. 그리고 다음의 산술 평균 $\overline{X}$ 는 가장 널리 사용되는 $\mu $의 추정치이다.

$\overline{X} =$true mean $\mu $의 추정치(우리가 구하는 값)$=\frac{1}{n}  \sum_{i=1}^n X_{i}  $ 이므로

$E( \bar{X})= \bar{X}$의 true mean 값$=E[ \frac{1}{n}  \sum_{i=1}^n  X_{i} ]$

$= \frac{1}{n}  \sum_{i=1}^n E( \mu + \varepsilon _{i})]= \frac{1}{n}[n \mu ]= \mu  $가 된다.

 

$Var( \bar{X} )=E[( \bar{X}-E( \bar{X})]^2=E[( \bar{X}- \mu )^2]$

$=E[( \frac{1}{n} \sum_{i=1}^n X_i- \mu )^2]$ $(∵ \bar{X}= \frac{1}{n} \sum_{i=1}^N X_i) $

$=E[( \frac{1}{n} \sum_{i=1}^n X_i- \frac{1}{n}n \mu )^2]=E[( \frac{1}{n} \sum_{i=1}^n (X_i- \mu ))^2 ]$

$=E[ \frac{1}{n^2}( \sum_{i=1}^n \varepsilon_i)^2]$ $(∵ X_i= \mu + \varepsilon_i)$

$=\frac{1}{n^2}E[( \varepsilon_1 + \varepsilon _2+ \cdots + \varepsilon _n)^2] $

$= \frac{1}{n^2} E[ \sum_{i=1}^n \varepsilon _i^2 +2 \sum_{i=1}^{n-1} \sum_{j>i}^n \varepsilon_i \varepsilon_j]$

$=\frac{1}{n^2}[ \sum_{i=1}^nE( \varepsilon_i^2)+2 \sum_{i=1}^{n-1} \sum_{j>i}^n E(\varepsilon_i \varepsilon_j)]$

$=\frac{1}{n^2} [n \sigma^2]$ $(∵ E( \varepsilon _{i} \varepsilon _{j})=0)$ $= \frac{ \sigma^2}{n} \cdots ①$

 

- ① 부분 보충 설명

$V( \varepsilon _i)=E( \varepsilon _i^2)-E[ \varepsilon_i]^2$ 인데,

$E(\varepsilon_i)=0$이므로 $V( \varepsilon _i)=E( \varepsilon _i^2)=\sigma^2$가 된다.

 

이를 통해 $\mu $의 추정치인 $\bar{X} $의 분포는 $\bar{X} \sim N( \mu , \frac{ \sigma^2 }{n})$라고 할 수 있다.

확률 변수 $\bar{X} $를 표준 정규 분포로 변환하면 $Z= \frac{ \bar{X}- \mu}{ \sqrt{ \frac{ \sigma^2}{n}}} \sim N(0,1) $가 된다.

 

Empirical Rule에 의하면 95%의 신뢰 구간은 $Prob[-1.96<Z<1.96]$일 때이다. 이를 이용하여 평균($\mu $)의 신뢰 구간을 구해보자.

$$Prob[-1.96<Z<1.96]=Prob[-1.96< \frac{ \bar{X}- \mu}{ \sqrt{ \frac{ \sigma ^2}{n} } }<1.96 ]$$

$$=Prob[ \bar{X}-1.96 \sqrt{ \frac{ \sigma^2 }{n}}< \mu < \bar{X} +1.96\sqrt{ \frac{ \sigma ^2}{n } } ]=0.95$$

[ t 분포(t Distribution) ]

모표준편차는 모집단의 평균을 알고 있어야 구할 수 있다. 즉 모평균은 모르고 모표준편차를 알고 있다는 가정은 다소 비현실적이며 실제로 모표준편차를 알 수 없는 경우가 대부분이다. 모표준편차를 모르는 상황에서 모평균을 추정할 수 있는 방법에 대해 알아보자.

 

이 전에 모표준편차가 알려져 있는 상황에서는 표본 평균의 분포는 아래와 같은 정규 분포를 따른다는 것을 중심 극한 정리(Central Limit Theorem)에 의해 알 수 있다. (관련 내용 모르시면 위의 정규 분포 관련 마지막 부분 설명 읽고 오세요.)

$\bar{X} \sim N( \mu, \frac{ \sigma }{ \sqrt{n}}) $ $(\mu=E(\bar{X}))$

 

t 분포는 모집단이 정규 분포를 따르더라도 true variance $ \sigma ^{2} $을 알기 어렵고 표본의 크기가 충분하지 않을 경우에 적용될 수 있다. 이는 정규 분포에서 평균의 해석에 많이 활용된다. t 분포는 아래 그림과 같이 0을 중심으로 대칭이고 종 모양을 하고 있다. 표준 정규 분포 곡선과 상당히 유사한 모양을 가지지만, 양 꼬리 부분에 상대적으로 많은 확률이 분포하고 있어 두꺼운 꼬리를 가지는 것이 차이점이다.

표준 정규 분포 곡선과 자유도에 따른 t 분포 곡선

자유도(=표본의 수-1)가 커질수록 표준 정규 분포와 모습이 점점 유사해진다.

 

모집단의 표준편차($\sigma$)를 모를 때 표본 표준편차($s$)를 적용할 수 있다.

$s^2= \frac{1}{n-1} \sum_{i=1}^n e_{i}^2 $

• $e_i$: 잔차(residual). $X_i-\bar{X}$. 표본(sample)으로 추정한 회귀식과 실제 관측값의 차이.

앞서 우리는 확률 변수 $\bar{X} $를 표준 정규 분포로 변환하는 방식에 대해 배웠다. 이 식의 $\sigma^2$를 $s^2$로 바꾸면 t 분포의 확률 변수를 정의할 수 있다. 즉, t 분포의 확률 변수는 아래와 같이 정의된다.

$t= \frac{ \bar{X}- \mu }{ \sqrt{ \frac{s^2}{n}}} \sim t_v$

• $t_v$: $v=(n-1)$. 정규 분포 모집단에서 추출한 표본 평균을 표본 표준편차로 표준화하면 자유도가 $n-1$인 t 분포의 형태를 띤다.

- t 분포의 신뢰 구간 추정

t 분포에서 신뢰 구간을 추정하는 것은 표준 정규 분포에서 신뢰 구간을 추정할 때와 유사하다. 다만 표준 정규 분포에서 신뢰 구간을 추정할 때는 z값을 사용한 대신, t 분포에서는 신뢰 구간을 추정할 때 t값을 사용한다.

 

신뢰 구간을 추정하기 앞서, 필요한 개념을 정리하고 넘어가려고 한다.

유의 수준(significance level)은 쉽게 말하자면 통계적인 가설 검정에서 사용되는 기준값이다. 일반적으로 유의 수준은 $α$로 표시하고 $α$%의 신뢰도를 기준으로 한다면 $(1- \frac{ \alpha }{100} )$ 값이 유의 수준 값이 된다. 가설 검정(hypothesis test) 절차에서 유의 수준 값과 유의 확률 값을 비교하여 통계적 유의성을 검증한다.

(유의 확률에 대한 설명은 여기에서 참고)

 

t 분포에서 특정 유의 수준 $α$에 대하여 $100(1-α)$%의 신뢰 구간은 아래와 같이 정리할 수 있다.

$$P(-t_{ \alpha/2}(n-1)< \frac{ \bar{X}- \mu}{ \frac{s}{ \sqrt{n}}} <t_{ \alpha/2}(n-1)=1- \alpha $$

$$P( \bar{X}-t_{ \alpha /2}(n-1) \frac{s}{ \sqrt{n}} < \mu < \bar{X}+t_{ \alpha/2}(n-1) \frac{s}{ \sqrt{n}}) =1- \alpha $$

t 분포표

df(degrees of freedom. 자유도)와 유의 수준($α$)을 통해 t 값을 구할 수 있다. 다만 신뢰 구간을 구할 때는 $\frac{ \alpha }{2} $ 값이 쓰이므로, t 분포표에서도 $100(1-α)$%의 신뢰 구간을 구할 때는 $\frac{ \alpha }{2} $에 대응하는 값을 봐야 한다. 예를 들면, 95%의 신뢰 구간을 추정하기 위해서는 α=0.25(2.5%)에 해당하는 값을 봐야 한다.

[ 통계적 가설 검정(Hypothesis Testing) ]

$Prob[ \bar{X}-1.98 \sqrt{ \frac{s^2}{n}}< \mu < \bar{X}+1.98 \sqrt{ \frac{s^2}{n}}]=0.95$

신뢰 수준 95%에서의 신뢰 구간은 위와 같이 구할 수 있다. 여기서 $(\bar{X}-1.98 \sqrt{ \frac{s^2}{n}})$은 95% 신뢰 구간에서의  lower bound(하한)이라 하고, $(\bar{X}+1.98 \sqrt{ \frac{s^2}{n}})$은 95% 신뢰 구간에서의 upper bound(상한)이라고 한다.

 

여기서 주의할 것이 true mean $\mu $ 값이 95% 신뢰 구간 안에 들어갈 확률은 95%가 아니라는 것이다. 결론부터 말하면 true mean $\mu $가 구간에 들어갈 확률은 0 또는 1이 된다. 신뢰 구간 안에 true mean이 존재한다면 확률은 1이 되고, 존재하지 않는다면 확률은 0이 된다.

 

기본적인 개념을 정리했으니, 본격적으로 통계적으로 가설을 검정하는 방법에 대해 배워보자.

1. 귀무가설(Null hypothesis) 설정(H0)

귀무가설의 정의는 "모집단의 특성에 대해 옳다고 제안하는 잠정적인 주장"이다. 귀무가설은 "모집단의 모수는 OO와 같다." 또는 "모집단의 모수는 OO와 차이가 없다."라고 가정하는 것이다. 즉, 귀무가설은 "~와 차이가 없다." "~의 효과는 없다." "~와 같다."라는 형식으로 설정된다.

 

어떤 분포에서 모평균을 $\mu_0=0$ 꼴로 추정했다고 하자. 이게 바로 귀무가설이 되는 것이다. 

2. 신뢰 수준과 표본 평균, 표본 표준편차를 이용하여 신뢰 구간 구하기

표본 평균 $\bar{X}=0.20$, 표본 표준편차 $s^2=1.0$, 표본의 크기 $n=100$이라고 가정하고 신뢰 수준이 95% 일 때의 신뢰 구간을 구하면 아래와 같다. (t 값은 1.98로 가정)

$[( \bar{X}-1.98 \sqrt{ \frac{s^2}{n}}), ( \bar{X}+1.98 \sqrt{ \frac{s^2}{n}})]=[0.002, 0.398]$

해당 신뢰 구간 안에 귀무가설 값 $\mu_0=0$이 들어갈 경우는 존재하지 않으므로 그 확률은 0%가 된다.

※ 오차 범위 안의 차이/오차 범위 밖의 차이

신문 기사를 보게 되면 오차 범위 밖. 오차 범위 안의 차이를 이야기할 때가 있다. 신문 기사에서 이야기하는 오차 범위는 표준 오차(standard error), $\pm \sqrt{ \frac{s^2}{n}}$를 말한다. 일반적으로 1,000~1,006 크기의 표본을 사용하여 표준 오차는 $\pm \sqrt{ \frac{s^2}{n}}= \pm 3.1$로 나오고, $\pm 1.98 \times 3.1= \pm 6.138$이 된다. 따라서 인기도 조사 등을 할 때 6.138보다 큰 차이면 오차 범위 밖 차이(통계적으로 유의한 차이), 6.138보다 작은 차이면 오차 범위 안 차이(통계적으로 유의하지 않은 차이)라고 한다.

- 통계적 오류(1종 오류, 2종 오류)

우리는 수집한 데이터를 바탕으로 어떠한 사안에 대하여 결정을 한다. 하지만 우리가 항상 옳은 결정을 하는 것은 아니다. 우리가 수집한 자료는 모집단에서 추출한 표본이기 때문에 항상 오류의 가능성이 존재하기 때문이다. 따라서 우리가 어떠한 의사 결정을 할 때에는 발생할 수 있는 오류를 최소화해야 한다. 통계적 가설 검정을 할 때에도 발생할 수 있는 통계적 오류를 최소화해야 옳은 판단을 할 확률을 높일 수 있다.

 

이제부터는 통계적 오류에 어떤 것이 있는지 살펴보려고 한다. 일단 통계적 오류에는 1종 오류와 2종 오류, 2가지 종류의 오류가 있다. 1종 오류와 2종 오류의 사전적 정의는 아래와 같다.

• 1종 오류(Type I error): 귀무가설(H0)이 실제로는 참이어서 채택해야 하는데 표본의 오차 때문에 이를 채택하지 않는 오류를 말한다. 보통 $α$로 표기하고 유의 수준이라고 부른다.
• 2종 오류(Type II error): 귀무가설(H0)이 실제로는 거짓이어서 채택하지 않아야 하는데 표본의 오차 때문에 이를 채택하는 오류를 말한다. 보통 $β$로 표기한다.

이 개념을 간단히 정리하면 아래의 표와 같이 나타낼 수 있다.

1종 오류 2종 오류 설명한 표

신뢰 수준이 95%으로 가설 검증을 시행한다고 생각해 보자. 신뢰 수준이 95%이므로 유의 수준 $α$는 5%가 된다. 따라서 제1종 오류가 발생할 확률은 항상 5%가 된다. 2종 오류는 신뢰 수준만으로는 정확하게 계산할 수 없다. (굳이 여기선 다루지 않음)

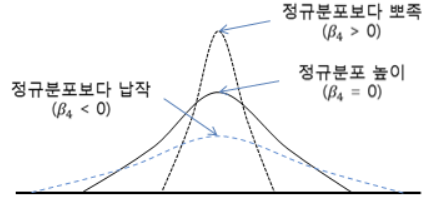
[ 첨도(Kurtosis) ]

첨도(Kurtosis)는 확률 분포의 꼬리가 두꺼운 정도를 나타내는 척도로, 관측치들이 얼마나 평균에 몰려 있는가를 측정할 때 사용한다. 첨도값이 3에 가까울수록 산포도가 정규 분포에 가까워진다. 첨도값에 따른 산포도를 정리하면 아래와 같다.

• 첨도값 < 3: 정규 분포보다 완만한, 납작한 형태
• 첨도값 = 3: 정규 분포를 가짐
• 첨도값 > 3: 정규 분포보다 더 뾰족한 분포

일반적으로 정규 분포의 첨도를 0으로 만들기 위해 3을 빼서 정의하는 경우도 있다. 이러한 정의를 excess kurtosis라고 한다. 이를 정리하면 아래의 그림과 같다.

첨도 값에 따른 산포도

[ 왜도(skewness) ]

분포의 비대칭도를 나타내는 통계량이다. 정규 분포, t 분포와 같이 대칭인 분포의 경우에는 왜도가 0이다.

왜도 부호에 따른 산포도

왜도의 부호에 따른 산포도는 위와 같이 나타난다.

 

이번 실습에서는 정규 분포에서 기초 통계량(평균, 표준편차, 분산 등)을 추출하는 프로그램을 작성해야 한다. 이제 이러한 프로그램을 작성하기 위해 필요한 SAS 개념을 짚고 넘어가자. 항상 말했듯이 이전의 실습에서 다룬 개념은 다루지 않습니다. 혹시 이 게시물에서는 다루지 않는 개념이지만, 코드에서 생소한 개념이 있을 때는 제 블로그에서 검색하시거나 SAS 카테고리 글 읽고 와 주시면 될 것 같습니다. (https://bing-su-b.tistory.com/category/Language/SAS)

[ RANNOR Function ]

SAS의 난수 함수를 이용하면 확률 변수를 생성할 수 있다. 그 외의 확률 변수를 생성하는 방법은 이 사이트를 참고하세요. RANNOR Function은 표준 정규 분포를 따르는 변량을 무작위로 생성하는 역할을 한다. standard NORmal distribution으로부터 RANdom 하게 난수를 생성한다고 하여 RANNOR 함수라고 기억하면 될 것 같다. 해당 함수의 문법을 정리하면 아래와 같다.

RANNOR(seed)

• seed: 난수를 생성하는 방법을 지시하는 숫자. seed 값이 같으면 나오는 결과 값이 모두 같다.
• seed 값의 범위: $seed<2^{31}-1$

[ SAS를 통해 기초 통계량을 뽑는 방법 ]

SAS에서 기초 통계량을 뽑은 Procedure는 크게 두 가지 1) PROC MEANS와 2) PROC UNIVARIATE가 있다. 이번 실습 때는 PROC UNIVARIATE에 대해 학습해 보려고 한다.

 

먼저 Univariate는 일변량(단변량),  즉 종속 변수(Y)가 1개라는 의미를 가진다. SAS 프로그램에서 PROC UNIVARIATE는 UNIVARIATE analysis(단변량 분석) PROCedure를 실행하겠다는 뜻이 된다.

- 명령어 정리

PROC UNIVARIATE DATA=xxx;  /* xxx라는 DATA를 불러와 UNIVARIATE Procedure 실행 */
	VAR x;  /* x 변수에 대한 통계 데이터를 분석 */
RUN;

UNIVARIATE Procedure를 실행하면 알고 싶은 변수들의 평균, 표준편차, 분산, 왜도,첨도 등 기초 통계량이 출력된다.

[ 표준 정규 분포에서 기초 통계량을 추출하는 프로그램 ]

DATA xbar;
	n=100;  /* 표본 크기: 100 */
	seed=1234;  /* seed 값을 1234로 설정 */
	mu=1.0;  /* true mean 값 지정 */
		DO i=1 TO n;
			e=RANNOR(seed);  /* 표준 정규 분포를 따르는 변량을 무작위로 생성 */
			x=mu+e;  /* Xi=μ+εi*/
			OUTPUT;  /* DO Loop 내부의 변수 값들을 모두 기억 */
		END;
RUN;

PROC UNIVARIATE DATA=xbar;
	VAR x;  /* x 변수에 대한 통계 데이터를 분석 */
RUN;

표본의 크기를 100, true mean의 값을 1.0이라고 지정하고, 확률 변수 e는 표준 정규 분포를 따른다고 가정하자. 이때, 확률 변수 x의 분포에 대한 여러 통계 데이터를 분석해 보는 프로그램이다. 이 프로그램을 실행하면 아래와 같은 결과를 얻을 수 있다. 

프로그램 실행 화면

seed 값을 똑같이 설정했다면, 동일한 결과가 나왔을 것이다. 여러 가지 통계 데이터가 출력된 것을 확인할 수 있고, 극 관측값에서의 관측값은 DO Loop 문 내부의 index-variable인 i 값이 된다.

 

이 프로그램에서 구해진 표본 평균과 표본 표준편차를 이용하여 신뢰 수준 95%에서의 신뢰 구간을 구하면 아래와 같다.

$=( \bar{X}-1.98 \sqrt{ \frac{s^2}{n} }, \bar{X}+1.98 \sqrt{ \frac{s^2}{n} })=(0.791101506, 1.239794454)$

 

귀무가설을 $\mu_0=0$로 세웠다면 95% 신뢰 수준에서의 신뢰 구간에 0이 포함되지 않으므로 이 귀무가설은 기각이 되어야 한다. 이 방법 외에도 t 값을 구하여 특정 귀무가설 $\mu_0$을 기각할지 채택할지를 결정할 수도 있다. 이 내용은 다음 게시물에서 다루려고 한다.(링크: https://bing-su-b.tistory.com/108)

[ 표준 정규 분포에서 표본 평균 직접 계산하기 ]

DATA xdata;
	n=200;  /* 표본 크기: 200 */
	seed=5678;  /* seed 값을 5678로 설정 */
	mu=10;  /* true mean 값 지정 */
	xsum=0;  /* 측정값을 기록하기 위한 변수 -> 초기화 */
		DO i=1 TO n;
			e=RANNOR(seed);  /* 표준 정규 분포를 따르는 변량을 무작위로 생성 */
			x=mu+e;  /* Xi=μ+εi*/
			xsum=xsum+x;  /* 측정값의 합 계산 */
			xbar=xsum/i;  /* i=1, 2, 3, ..., 200까지 표본 평균을 구함. */
			OUTPUT;  /* DO Loop 내부의 변수 값들을 모두 기억 */
		END;
RUN;

PROC UNIVARIATE DATA=xdata;
	VAR x;  /* x 변수에 대한 통계 데이터를 분석 */
RUN;

PROC PRINT DATA=xdata;
	VAR i xsum xbar;  /* i, xsum, xbar 변수를 불러와서 PRINT Procedure 실행 */
RUN;

표본의 크기를 200, true mean 값을 10이라고 지정하고, 확률 변수 e는 표준 정규 분포를 따른다고 가정하자. 이 프로그램의 전반적인 Logic을 정리하면 다음과 같다. 먼저 DO Loop 문을 돌면서 표본 평균을 직접 계산하고 있다. 그리고, UNIVARIATE Procedure를 통해 분석된 확률 변수 x의 분포에 대한 여러 통계 데이터를 분석하고 있다. 마지막으로는 직접 계산한 표본 평균을 출력한다. 이를 통해 UNIVARIATE Procedure에서 분석된 표본 평균과 직접 계산한 표본 평균이 같은지를 비교할 수 있게 된다. 이 프로그램을 실행하면 아래와 같은 결과를 얻을 수 있다.

프로그램 실행 화면

프로그램 실행 결과를 살펴보면 UNIVARIATE Procedure를 통해 분석된 평균은 9.9386이고, 반복문을 통해 최종적으로 계산된 표본 평균 역시 9.9386으로 동일한 것을 확인할 수 있다.

[ 신뢰 수준 95%에서의 신뢰 구간을 계산하는 프로그램 ]

DATA normal;
	n=10000;
	mu=1;  /* true mean 값 지정 */
	seed=1234;  /* seed 값을 1234로 지정 */
	DO obs=100 TO n BY 100;
		xsum=0;  /* 측정값을 기록하기 위한 변수 -> 초기화 */
		esqsum=0;  /* 측정값을 기록하기 위한 변수 -> 초기화 */
		obs1=obs-1;  /* 표본 표준편차를 계산하기 위해 (표본 크기-1)을 해 줌. */
		DO i=1 TO obs;
			e=RANNOR(seed);  /* 표준 정규 분포를 따르는 변량을 무작위로 생성 */
			x=mu+e;  /* Xi=μ+εi */
			xsum=xsum+x;  /* 측정값의 합 계산 */
			esqsum=esqsum+e**2;  /* 편차(x-mu) 제곱들의 합 -> 분산 계산에 사용 */
            END;
		xbar=xsum/obs;  /* 표본 평균 계산 */
		ssq=esqsum/obs1;  /* 표본 분산 계산 */
		lowb=xbar-1.98*SQRT(ssq/n);  /* 신뢰 구간의 하한 계산 */
		uppb=xbar+1.98*SQRT(ssq/n);  /* 신뢰 구간의 상한 계산 */
		OUTPUT;  /* 첫 번째 DO Loop 내부의 변수 값들을 모두 기억 */
	END;
RUN;

PROC UNIVARIATE DATA=normal;
	VAR x;  /* x 변수에 대한 통계 데이터를 분석 */
RUN;

PROC PRINT DATA=normal;
	VAR obs lowb xbar uppb;  /* obs, lowb, xbar, uppb 변수를 불러와서 PRINT Procedure 실행 */
RUN;

해당 프로그램은 표본의 크기를 100부터 시작하여 100씩 늘려가며, 확률 변수 x의 분포에 대한 여러 통계 데이터를 관찰하고 신뢰 수준이 95% 일 때의 신뢰 구간을 구하고 있다. 이 프로그램을 실행하면 아래와 같은 결과를 얻을 수 있다.

프로그램 실행 결과

obs=10000일 때 표본 평균은 1.00584로 계산된다. 이는 UNIVARIATE Procedure에 의해 분석된 평균 0.90912보다 $\mu=1$에 더 근접한다.