고정 헤더 영역
상세 컨텐츠
본문
반응형
SMALL
세 번째 실습으로는 이산 확률 분포의 일종인 이항 분포와 푸아송 분포에서의 확률을 계산하는 프로그램을 작성해 봤다. 저번 게시글과 마찬가지로 프로그램 작성을 위해 필요한 통계 개념을 먼저 짚고 넘어가려고 한다.
[ 이항 분포(Binomial Distribution) ]
베르누이 분포는 시행 횟수를 딱 한 번만 고려한 것이다. 이때 시행을 여러 번 했을 때는 이항 분포가 된다. 즉, 이항 분포의 확률변수 X는 베르누이 시행을 n번 했을 때, 성공한 횟수를 말한다. 이는 서로 독립이고 동일한 베르누이 분포를 따르는 n개의 확률변수 $X_{1}, \cdots , X_{n} $을 모두 더한 것 $X= \Sigma X_{i} $가 이항 확률변수가 된다. 이때, X는 $Binomial(n, p)$를 따른다고 말한다.
베르누이 분포에 대한 내용 참고: https://bing-su-b.tistory.com/105
[ SAS ] - 베르누이 분포에서 데이터를 생성하고 표본 평균(xbar)을 구하는 프로그램 작성
두 번째 수업 실습으로 진행한 "표본 평균(xbar)"을 구하는 프로그램을 작성해 봤다. 첫 번째 프로그램은 동전 던지기 분포에서 데이터를 생성하고 표본 평균(xbar)을 구하는 프로그램이다. 프로그
bing-su-b.tistory.com
[ 푸아송 분포(Poisson Distribution) ]
어떤 단위 구간(시간)에서 일어나는 특정 사건의 발생 횟수 분포에 관한 것이 푸아송 분포다. 푸아송 분포를 통해서는 특정 구간(시간)에서 평균 발생 횟수는 알 수 있지만, 그 구간 내 각 사건은 랜덤으로 일어나기 때문에 정확한 타이밍을 예측할 수 없다. 즉, 구간 내 사건이 랜덤으로 발생하지 않고 어떠한 규칙에 의해 발생한다면 푸아송 분포라고 할 수 없다. 이것 만이 아니라, 푸아송 분포를 따른다고 말할 수 있으려면 사건의 발생 횟수는 아래의 성질들을 만족해야 한다.
- 서로 겹치지 않는 단위 구간(시간)에서 발생한 사건들은 서로 독립이다.
- 단위 구간(시간)에서 사건이 발생한 횟수는 단위 구간(시간)의 크기에 비례하고, 외부의 영향을 받지 않는다.
- 같은 사건이 거의 동시에 일어날 확률은 0이다.
어떤 사건이 위의 세 가지 성질을 만족하면서 일어나면 이 사건은 푸아송 확률 과정을 따른다고 한다. 여기서 '확률 과정'은 시간과 관련되어 확률적인 성격을 가진다는 것을 의미한다. 간단히 말하자면, 시간에 따라 확률이 변한다고 이해하면 된다. 평균 발생 횟수가 $ \lambda $인 푸아송 확률 변수의 확률 밀도 함수는 아래와 같다.
$$f_{X}(x)= \frac{ \lambda ^{x} e^{- \lambda } }{x!} , x=0, 1, 2, \cdots $$
[ 이항 분포의 푸아송 분포로의 근사 ]
이항 분포는 특정한 조건 하에서 푸아송 분포로 근사할 수 있다.
$$P(x)= \frac{ \lambda ^{x} e^{- \lambda } }{x!} (Poisson) \approx P(x)= \frac{n!}{x!(n-x)!} p^{x} (1-p)^{n-x} (Binomial)$$
위의 근사 식은 이항 분포의 n이 매우 크고, p가 0에 가까울 때 이용할 수 있다. 이때, n개의 베르누이 시행에서 x개의 성공 확률은 $np= \lambda $인 푸아송 분포로 근사할 수 있다.
※ 이항 분포의 푸아송 분포로의 근사 예시 문항
Example 1) 어떤 사람이 30년 동안 직장을 오가는 동안 교통사고가 발생할 확률을 알고 싶어 한다고 가정하자. 만약 그녀가 일년에 250일, 30년 동안 매일 왕복한다면 그녀는 30년 동안 15,000번을 왕복하게 될 것이다. 주행 중 사고가 발생할 확률을 p=0.0001이라고 하자. 그렇다면 근사를 사용하여 사고가 x번 일어날 때의 확률을 쉽게 계산할 수 있다.
n = 15,000 trips, 사고 확률 p=0.0001, λ = np = 15000 x 0.0001 = 1.5
- P(0): $by Binomial= \frac{15000!}{0!15000!} 0.0001^{0} 0.9999^{15000}=0.22311$
$by Poisson= \frac{1.5^0 e^{-1.5} }{0!}=0.22$
- P(1): $by Binomial= \frac{15000!}{1!14999!}(0.0001)^1(0.9999)^{14999}=0.33470$
$by Poisson= \frac{1.5^1 e^{-1.5}}{1!}=0.33$
Example 2) 잠수함이 비교적 일정한 길이(약 60일)의 임무를 수행한다고 가정하자. 각 임무 동안 잠수함은 예비 부품 공급에 의존해야 한다. 임무가 끝나면, 입찰자는 잠수함 보급품에서 꺼낸 아이템을 보충한다. 이러한 경우에는 특정 유형의 부품 고장이 임무 수행 중에 x번 발생할 확률은 $P(x)= \frac{( \lambda \Delta )^x e^{-( \lambda \Delta) } }{x!} $이다.
(Δ: 임무 기간, λ: 특정 유형의 부품에 대한 단위 시간당 평균 고장 횟수)
61번째 폴라리스 잠수함 순찰 후 λΔ는 1.0으로 추정된다. 그런 다음 아래의 식을 사용하여 특정 유형의 부품 고장 횟수 x의 확률을 계산할 수 있다.
$$ P(0)= \frac{1^0e^{-1}}{0!} \approx 0.3679 ㅤP(1)= \frac{1^1e^{-1}}{1!} \approx 0.3679ㅤP(2)= \frac{1^2e^{-1}}{2!} \approx 0.1839\\ P(3)= \frac{1^3e^{-1}}{3!} \approx 0.0613 P(4)= \frac{1^4e^{-1}}{4!}=0.0613$$
이번 실습에서는 이산 확률 분포에서의 확률을 구해야 하는 프로그램을 작성해야 한다. 이제 이러한 프로그램 작성을 위하여 필요한 SAS 개념을 짚고 넘어가자. (저번 실습 때 다룬 내용에 대해서는 다루지 않습니다! 혹시 이 게시물에서는 다루지 않는 개념이지만, 생소한 개념이 있으시다면 이 링크로 접속하여 개념 확인하고 와 주시면 됩니다.)
[ 단순 IF 구문 ]
IF란 '만약 ~라면'이라는 의미다. SAS에서는 이를 조건부 문장으로 활용하여 데이터를 편집하는 하나의 기준을 제시한다.
- 명령어 정리
IF XXX=N; /* 숫자 칼럼 XXX가 N인 행들만 선택 */
IF YYY='ZZ'; /* 문자 칼럼 YYY가 ZZ인 행들만 선택 */
IF PPP^=N; /* 숫자 칼럼 PPP가 N이 아닌 행들만 선택(^=) */
IF XXX=N AND YYY='ZZ'; /* 칼럼 XXX가 N이고 칼럼 YYY가 ZZ인 행을 선택(AND, OR) */
IF XXX IN (N1, N2); /* 칼럼 XXX가 N1이거나 N2인 행을 선택(IN, NOT IN) */※ AND. OR
- (1) AND (2): (1)이면서 (2)인 값들을 선택하는 것. 교집합 개념.
- (1) OR (2): (1)이거나 (2)인 값들을 선택하는 것. 합집합 개념.
※ IN, NOT IN
- IN: OR의 개념과 동일. OR로 할 때보다 명령어의 길이를 줄일 수 있어서 자주 사용됨.
- NOT IN(N1, N2): NOR(NOT+OR)의 개념과 동일. 즉, N1과 N2가 아닌 행을 선택.
※ SAS 프로그램 시 주의할 점(문자 vs 숫자)
SAS 프로그램에서는 숫자 칼럼 내부 데이터를 선택할 때 숫자를 그대로 쓰고, 문자 칼럼 내부 데이터를 선택할 때는 ' '를 붙인다. 따옴표를 붙이지 않을 경우 에러가 발생할 수 있으니 주의하자.
[ IF 구문을 활용한 칼럼 변환 ]
IF~THEN~의 형식으로 특정 조건(IF문)을 제시하고 그 조건에 부합하는 행에 따라 변화(THEN)를 줄 수 있다. 테이블을 가공할 때나 특정 상황에서 칼럼을 변환할 때 이용하면 좋다.
- 명령어 정리
IF XXX=N THEN YYY+2; /* 칼럼 XXX가 N이면 칼럼 YYY에 2를 더한 값을 출력 */
IF XXX=N THEN DELETE; /* 칼럼 XXX가 N이면 해당 행을 삭제 */
IF XXX=N THEN NEW='새로운칼럼';
/* 칼럼 XXX가 N이면 NEW를 생성하고 '새로운칼럼'이라는 값이 나오도록 만듦 */
IF XXX=N THEN NEW=YYY+2; ELSE NEW=ZZZ+3;
/* 칼럼 XXX가 N이면 칼럼 YYY에 2를 더한 값을 출력 */
/* XXX가 N이 아닌 나머지의 경우 ZZZ에 3을 더한 값을 출력 */[ PROBBNML Function ]
PROBBNML 함수는 PROBability+BiNoMiaL의 약자로, 이항 분포의 확률을 계산하는 함수다.
PROBBNML 함수의 기본 문법을 정리하면 아래와 같다.
PROBBNML(p, n, m)- p: 성공 확률을 지정하는 숫자 상수, 변수 또는 식.
- n: 독립적인 베르누이 시행의 정수를 지정하는 숫자 상수, 변수 또는 식.
- m: 성공 횟수를 정수로 지정하는 숫자 상수, 변수 또는 식.
$$ PROBBNML(p, n, x)= \frac{n!}{0!(n-0)!}p^0(1-p)^{n-0}+ \frac{n!}{1!(n-1)!}p^1(1-p)^{n-1}\\+ \cdots + \frac{n!}{x!(n-x)!}p^x(1-p)^{n-x} $$
PROBBNML 함수를 이용하면 0부터 x까지의 누적 확률이 계산된다. 따라서 x번째의 단독 확률을 구하고 싶을 때는 PROBBNML(p, n, x)-PROBBNML(p, n, x-1)을 하여 누적 확률을 단독 확률로 전환해야 한다. 이때, P(x=0)은 PROBBNML(p, n, 0)을 해주면 되기 때문에 단독 확률을 구할 경우에는 x=0인 경우와 x=0이 아닌 경우로 나누어 구해야 한다.
[ POISSON Function ]
말 그대로 푸아송 분포의 확률을 반환하는 함수이다. 해당 함수의 문법을 정리하면 아래와 같다.
POISSON(λ, x)- λ: 평균 발생 횟수
- x: 발생 횟수(x번). 정수형 랜덤 변수
PROBBNML 함수와 마찬가지로 POISSON 함수 역시 이용하면 0부터 x까지의 누적 확률이 계산된다. 따라서 x번째의 단독 확률을 구하고 싶을 때는 POISSON(λ, x)-POISSON(λ, x-1)을 하여 누적 확률을 단독 확률로 전환해야 한다. 이때, P(x=0)은 POISSON(λ, 0)을 해주면 되기 때문에 단독 확률을 구할 경우에는 x=0인 경우와 x=0이 아닌 경우로 나누어 구해야 한다.
[ 여러 가지 통계량을 테이블로 출력시키는 방법 ]
PROCedure TABULATE를 통해 여러 가지 요약 통계량들을 다양한 테이블의 형태로 출력할 수 있다.
- 명령어 정리
PROC TABULATE DATA=xxx; /* xxx라는 DATA를 불러와 TABULATE Procedure 실행 */
CLASS yyy zzz; /* yyy와 zzz를 테이블에 작성할 변수로 지정 */
TABLE aaa, bbb; /* aaa를 행 변수, bbb를 열 변수로 둠 */※ 통계량에 대한 출력 포맷 지정
TABULATE Procedure에서는 다양한 통계량들을 출력할 수 있다. 이때, 사용자는 *F=Format 형식을 이용하여 통계량에 출력 포맷을 지정할 수 있다. *F=5.0는 전체 자릿수를 5자리, 소수점의 자릿수를 0자리로 지정한 것이다. 이와 같은 출력 포맷의 지정은 각 cell의 넓이에도 영향을 준다.
※ 계층적 구조를 가지는 테이블의 작성
TABLE 명령문에서는 단순히 변수를 나열하는 것 외에도 ( ) 또는 *를 사용하여 다양한 출력 형식을 사용할 수 있다.
PROC TABULATE data=xxx;
CLASS aaa bbb ccc;
TABLE (aaa bbb ccc)*F=7.1; /* 단순한 나열식 구조의 테이블 출력. */
TABLE aaa*bbb*ccc*F=4.1; /* aaa bbb ccc의 순서로 계층적 구조를 가지는 테이블 출력 */
TABLE aaa*(bbb ccc)*F=4.1; /* aaa 변수 아래에 bbb ccc가 나열식 구조를 가지는 테이블 출력 */
RUN;[ 이항 분포의 확률을 계산하는 프로그램 ]
DATA binomial;
ps=0.5; /* 성공 확률이 0.5라고 정의 */
n=4; /* 총 시행 횟수 */
DO x=0 TO n;
/* 조건문 Logic은 위의 PROBBNML 함수 설명 참고 */
IF x=0 THEN p=PROBBNML(ps, n, x);
ELSE p=PROBBNML(ps, n, x)-PROBBNML(ps, n, x-1);
OUTPUT; /* DO Loop 내부의 변수 값들을 모두 기억 */
END;
RUN;
PROC PRINT DATA=binomial;
VAR x p; /* x와 p 변수를 불러와서 PRINT Procedure 실행 */
RUN;성공 확률을 0.5라고 지정한 후, 총 4번의 시행에서 성공 횟수에 따른 확률을 구하는 프로그램이다. 이 프로그램을 실행하면 아래와 같은 결과를 얻을 수 있다.
Example 1) 어떤 사람이 30년 동안 직장을 오가는 동안 교통사고가 발생할 확률을 알고 싶어 한다고 가정하자. 만약 그녀가 일 년에 250일, 30년 동안 매일 왕복한다면 그녀는 30년 동안 15,000번을 왕복하게 될 것이다. 주행 중 사고가 발생할 확률을 p=0.0001이라고 하자.
이항 분포를 푸아송 분포로 근사하는 내용을 설명하며 들었던 예시다. 사고가 최대 5번 난다고 가정했을 때, 이항 분포를 활용하여 30년 동안 차 사고가 날 확률을 구하는 프로그램을 작성해 보자.
DATA binomial;
ps=0.0001; /* 사고 발생 확률 */
n=15000; /* 1년에 500번 왕복*30년. 왕복하는 차의 대수 */
ac=5; /* 사고 횟수 */
DO x=0 TO ac;
IF x=0 THEN p=PROBBNML(ps, n, x);
ELSE p=PROBBNML(ps, n, x)-PROBBNML(ps, n, x-1);
OUTPUT;
END;
RUN;
PROC PRINT DATA=binomial;
VAR x p;
RUN;이 프로그램을 실행하면 아래와 같은 결과를 얻을 수 있다.
출퇴근할 때 사고가 한 번 날 확률 0.33470이 가장 크다는 것을 알 수 있다.
[ 성공 확률이 달라질 경우 이항 분포 확률 계산 ]
DATA binomial;
pn=0.6; /* 최대 성공 확률 */
p1=0.1; /* 최소 성공 확률 */
n=10; /* 베르누이 시행 횟수 */
DO ps=p1 TO pn BY 0.1; /* 성공 확률을 0.1씩 증가하며 관찰 */
DO x=0 TO n; /* 성공 횟수에 따른 확률 계산하는 반복문 */
IF x=0 THEN p=PROBBNML(ps, n, x);
ELSE p=PROBBNML(ps, n, x)-PROBBNML(ps, n, x-1);
OUTPUT; /* DO Loop 내부의 변수 값들을 모두 기억 */
END;
END;
RUN;
PROC TABULATE DATA=binomial; /* binomial DATA를 불러와 TABULATE Procedure 실행 */
CLASS x ps; /* x와 ps를 테이블에 작성할 변수로 지정 */
VAR p; /* p 변수의 값을 불러옴 */
/* *F=8.4: 숫자 길이-8, 소수점 다음 4자리로 포맷 지정 */
TABLE x, ps*p*sum*F=8.4; /* x: 행 변수, ps, p, sum: 열 변수. 해당 순서대로 계층 구조를 가짐 */
RUN;성공 확률이 0.1부터 0.6까지 0.1씩 증가할 때 각 확률에서 성공 횟수에 따른 이항 분포의 확률을 구하는 프로그램이다. 이 프로그램을 실행하면 아래와 같은 결과를 얻을 수 있다.
[ 푸아송 분포의 확률을 계산하는 프로그램 ]
DATA poisson;
ambda=5; /* ambda는 λ(평균 발생 횟수)를 의미 */
n=10; /* 발생 횟수 최댓값 */
DO x=0 TO n; /* x: 사건 발생 횟수 */
/* POISSON 분포 확률 구하는 Logic은 POISSON 함수 설명 참고 */
IF x=0 THEN prob=POISSON(ambda, x);
ELSE prob=POISSON(ambda, x)-POISSON(ambda, x-1);
OUTPUT; /* DO Loop 내부의 변수 값들을 모두 기억 */
END;
RUN;
PROC PRINT DATA=poisson;
VAR x prob; /* x, prob 변수의 값들을 불러옴 */
RUN;평균 발생 횟수가 5인 푸아송 분포에서 사건의 발생 횟수에 따른 푸아송 분포의 확률을 계산하는 프로그램이다. 이 프로그램을 실행하면 아래와 같은 결과를 얻을 수 있다.
[ 평균 발생 횟수(λ)가 달라질 경우 푸아송 분포 확률 계산 ]
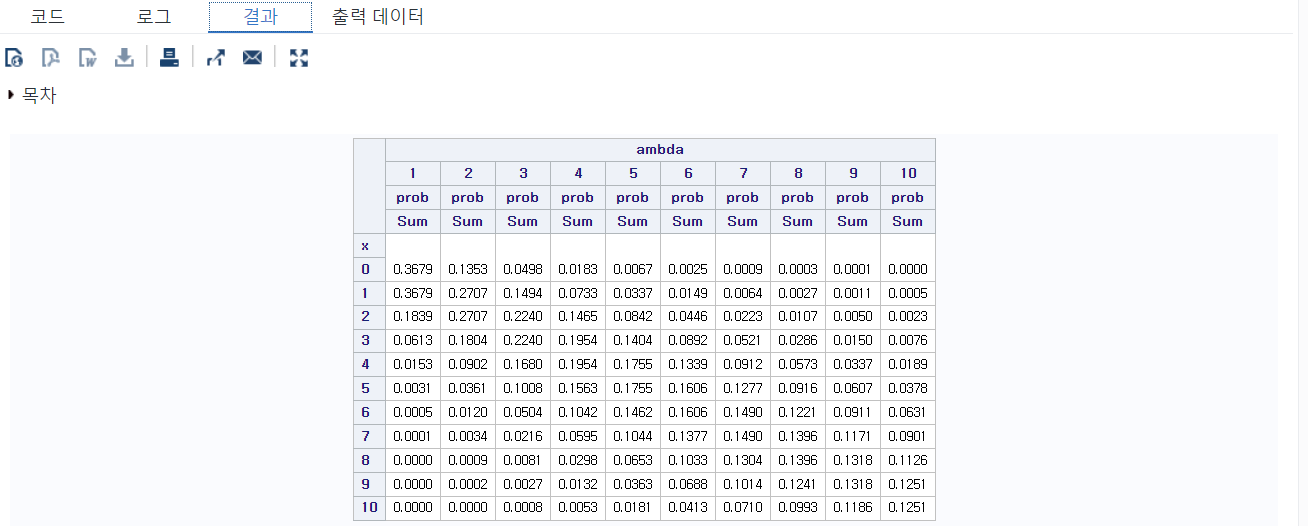
DATA poisson;
ambdan=10; /* 평균 발생 횟수(λ)의 최댓값 */
n=10; /* 발생 횟수의 최댓값 */
DO x=0 TO n; /* x: 발생 횟수를 1씩 늘려감 */
DO ambda=1 TO ambdan; /* 평균 발생 횟수를 1부터 10까지 1씩 늘려감 */
/* 푸아송 분포의 확률 계산. Logic은 POISSON 함수 설명 참고 */
IF x=0 THEN prob=POISSON(ambda, x);
ELSE prob=POISSON(ambda, x)-POISSON(ambda, x-1);
OUTPUT; /* DO Loop 내부의 변수들 값 기억 */
END;
END;
RUN;
PROC TABULATE DATA=poisson; /* poisson DATA를 불러와 TABULATE Procedure 실행 */
CLASS x ambda; /* x와 ambda를 테이블에 작성할 변수로 지정 */
VAR prob; /* prob 변수의 값을 불러옴 */
/* *F=8.4: 숫자 길이-8, 소수점 다음 4자리로 포맷 지정 */
TABLE x, ambda*prob*sum*F=8.4; /* x: 행 변수 */
/* ambda, prob, sum: 열 변수. 해당 순서대로 계층 구조를 가짐 */
RUN;평균 발생 횟수(λ)가 1부터 10까지 증가할 때 각 사건의 발생 횟수 별로 푸아송 분포의 확률을 구하는 프로그램이다. 이 프로그램을 실행하면 아래와 같은 결과를 얻을 수 있다.
반응형
LIST
'Language > SAS' 카테고리의 다른 글
| [ SAS ] - 평균 회귀 모형에서 기초 통계량을 추출하는 프로그램 작성 + 가설 검정 (0) | 2023.04.21 |
|---|---|
| [ SAS ] - 정규 분포에서 기초 통계량을 추출하는 프로그램 작성 (0) | 2023.04.15 |
| [ SAS ] - 베르누이 분포에서 데이터를 생성하고 표본 평균(xbar)을 구하는 프로그램 작성 (0) | 2023.03.31 |
| [ SAS ] - DATA를 입력하고, sorting하는 프로그램 작성 (0) | 2023.03.20 |
| [ SAS ] - 언어에 대한 소개 및 SAS Studio 설치 방법 (4) | 2023.03.16 |
댓글 영역