고정 헤더 영역
상세 컨텐츠
본문
두 번째 수업 실습으로 진행한 "표본 평균(xbar)"을 구하는 프로그램을 작성해 봤다.
첫 번째 프로그램은 동전 던지기 분포에서 데이터를 생성하고 표본 평균(xbar)을 구하는 프로그램이다.
프로그램 작성을 위해 필요한 통계 개념을 짚고 넘어가자.
[ 베르누이 분포(Bernoulli Distribution) ]
베르누이 시행(Bernoulli Trial)은 '성공'과 '실패'의 두 가지 결과만이 존재하며 각 시행은 서로 독립이다.
대표적인 예시가 동전 던지기이다. 동전을 던지면 앞면이 나오거나 뒷면이 나오거나 둘 중 하나이고, 동전을 반복적으로 던졌을 때 먼저 시행에서 앞면이 나왔다고 하여 그 다음 시행에서 뒷면이 나올 확률이 높아지거나 이러지는 않는다. 즉, 각 시행은 서로에게 영향을 주지 않고 독립이다. 이항 분포 역시 베르누이 시행을 전제로 하고 있다.
한 베르누이 시행에서 어떤 확률 변수 X가 '성공'이면 1, '실패'면 0의 값을 갖는다고 하자. 이 확률변수 X를 베르누이 확률변수라고 하고, 이 분포를 베르누이 분포라고 한다. 시행의 결과가 '성공'일 확률을 p라고 하면, X는 $Bernoulli(p)$를 따른다고 말한다.

확률변수의 기댓값과 분산을 구하면 아래와 같다.

즉, 성공할 확률 그 자체가 베르누이 확률변수의 기댓값이 되는 것을 확인할 수 있다.
이번 실습은 모집단 수에서 일정한 수만큼 추출하는 sampling을 진행한 후 데이터 집합을 나타내는 프로그램을 작성해야 한다. 이러한 프로그램을 작성하기 위해 필요한 SAS 개념을 짚고 넘어가자.
[ 반복 DO 명령어(DO loop 문) ]
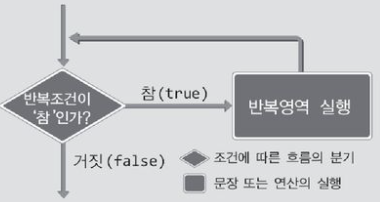
SAS에서 Do loop 문의 개념을 설명하기 위해 C언어에서 학습했던 while 문의 flow chart(순서도)를 가져왔다. C언어의 반복문 중 하나인 while 반복문은 조건식이 참일 때까지 반복 영역에 있는 코드를 계속 반복하여 실행하고, 거짓이면 반복문을 끝낸 후 다음 코드를 실행한다. (자세한 설명이 궁금하신 분은 이 사이트를 참고하시면 됩니다.)
- SAS Language에서 반복문 구현
DO index-variable=start TO stop <BY increment>;
// 초기값(start) 부터 stop 값까지 incerment만큼 증가하면서 반복문 진행
/* SAS statements */
OUTPUT; // OUTPUT을 넣으면 각 단계의 결과를 모두 출력.
// OUTPUT을 넣지 않으면 최종 값을 출력
END; // 반복문 끝(DO와 END는 짝을 이룬다.)SAS에서의 반복문 역시 C언어와 마찬가지로 조건식이 참일 동안 반복 영역에 있는 코드를 계속 반복하여 실행한다. 이때, BY 옵션을 추가하면 index-variable의 증감 단위를 지정할 수 있다. 만약 increment를 지정하지 않으면, index-variable은 기본적으로 1씩 증가하게 된다.
※ SAS DO Loop 문의 조건식에서 변수 값 관찰(OUTPUT X)
DATA ex;
obs=10;
p=0.5;
xsum=0;
DO i=1 TO obs;
x=RAND('BERNoulli', p);
xsum=xsum+x;
END;
xbar=xsum/obs;
RUN;
PROC PRINT DATA=ex;
VAR i obs xsum xbar;
RUN;위와 같은 프로그램을 실행하면 아래와 같은 결과가 출력된다.

SAS의 DO Loop 문은 조건식이 참일 동안 코드를 계속 반복해서 실행하는 반복문이다. 위의 코드에서 반복문(DO Loop 문)의 실행 과정에 대해 간단하게 짚어보자.
- 조건식을(i=1부터 10(obs 값)인지를) 평가한다.
- 조건식이 참이면 실행문(반복 코드)을 실행한다.
- 실행문이 한 번 실행될 때마다 i는 1씩 증가한다.
- i 값 갱신 후 다시 조건식으로 되돌아가 조건식을 평가한다.
- 조건식이 참이면 1~3을 반복하고, 아니면 반복문을 종료(END)한다.
위의 과정이 9번 반복되면(반복문이 9번 실행되면) i=10이 된다. 이 떄를 생각해보자. i=10이면 일단 조건식에는 부합하므로 반복문이 한 번 더 실행되어 반복문은 총 10번 실행되게 된다. 이 때의 반복문이 끝나면 i=11로 갱신되고, 다시 조건식으로 되돌아가 조건식을 평가한다. i=11일 때는 조건식이 성립하지 않으므로 반복문이 종료(END)된다. 즉, i=11인 채로 반복문이 종료되기 때문에 최종 i 값을 출력하면 11이 나오게 된다.
※ SAS DO Loop 문의 조건식에서 변수 값 관찰(OUTPUT O)
DATA ex;
obs=10;
p=0.5;
xsum=0;
DO i=1 TO obs;
x=RAND('BERNoulli', p);
xsum=xsum+x;
OUTPUT;
END;
xbar=xsum/obs;
RUN;
PROC PRINT DATA=ex;
VAR i obs xsum xbar;
RUN;위와 같은 프로그램을 실행하면 아래와 같은 결과가 출력된다.

앞서 살펴본 프로그램과 다른 점이 있다면, 해당 프로그램에서는 DO Loop의 END 전에 OUTPUT; 구문이 존재한다. OUTPUT 명령어는 변수의 값을 계속 저장한 채 반복문을 돌기 때문에, 해당 명령어를 사용하면 반복문이 반복하는 과정을 모두 관찰할 수 있다. 이 때 역시, 위의 프로그램과 마찬가지로 반복문이 10번 돌고, i=11일 때 조건식에 부합하지 않으므로 반복문이 종료(END)된다. 하지만, OUTPUT이 반복문 내부에 있기 때문에 반복문이 끝나기 전까지의 i, obs, xsum 값이 테이블에 입력된다. 따라서 i 값은 반복문이 끝나기 직전 값인 10까지만 출력된다.
또한, 출력 화면에서 표본 평균(xbar) 값은 출력되지 않는 것을 볼 수 있다. i, obs, xsum 변수의 값은 반복문을 10번 돌며 값이 10개로 생성되지만, xbar 변수의 값은 반복문이 끝나고 단 한 번 생성된다. 즉, DO Loop 문 내부에서 생성되어 값이 여러개인 변수와 값이 반복문 외부에서 생성되어 값이 한개인 변수가 있다면, 값이 한개인 변수는 인식되지 못하고 값이 여러개인 변수만 출력된다.
[ 변수 사용하기 ]
프로그래밍을 하며 값을 다루기 위해서 변수가 필요할 때가 있다. 본격적으로 프로그램을 작성하기 전에 변수를 생성하고 값을 저장하는 방식에 대해 간단하게 알아보자. 변수는 말 그대로 바뀔 수 있는 값이고, 영어로는 variable이라고 한다. 쉽게 생각하자면, 바뀔 수 있는 어떠한 값을 보관하는 역할을 수행하는 것이 변수라고 할 수 있겠다.
- SAS에서 변수를 생성하고 값을 할당하는 방법
new-variable = expression; // 새로운 열(column) 생성
existing-variable = expression; // 기존 열(column) 내용 변경SAS 문법은 위에서 아래의 순서대로 해석이 되는 절차지향을 따른다. 따라서 변수를 사용하여 새로운 열(column)을 생성하기 위해서는 변수를 직접적으로 사용하는 부분보다 위에 변수를 선언해줘야 한다. 즉, 변수를 선언한다는 것은 변수가 있다는 것을 알려준다는 뜻이기도 하다.

변수에 값을 저장하는 방식을 "변수에 값을 할당한다"라고 한다. 일반적으로 수학에서의 "="는 "같다"는 뜻이지만, 프로그래밍에서 "="는 값을 할당할 때 사용한다. 따라서 num1 = 10;은 num1과 10이 같다는 뜻이 아니라 num1에 10을 할당(저장)한다는 뜻이 된다.
이제 변수를 표현할 때 자주 사용하는 표현법 몇 가지를 살펴보자.
1. 상수 표현
- 날짜 상수를 통해 변수에 날짜 값을 부여하는 경우
: SAS에서 날짜 형태로 상수를 표현하기 위해서는 따옴표와 character D를 추가하면 된다.
StudyDay = '31MAR2023'D;
// 2023년 3월 31일의 SAS 날짜 값과 동일한 StudyDay 변수 생성- 문자 상수: 채우고 싶은 값을 따옴표 사이에 넣어서 표현한다.
host = 'SAS'; // host 변수에 SAS 값(문자열) 할당- 숫자 상수: 변수명 = 숫자꼴로 변수에 값 할당 (단, 숫자는 정수 or 소수)
p = 0.5; // p 값에 0.5 값을 할당2. 연산자(산술 연산자만 정리)
SAS에서 쓰이는 산술 연산자를 정리하면 아래와 같다. (비교 연산자는 추후에 나오면 정리)
| 기능 | 예시 | 우선 순위 | |
| ** | 지수 계산 | x1 = x**x (x^x와 동일) | 1 |
| - | 부호 변동 | x2 = -x | 1 |
| * | 곱하기 | x3 = x*y | 2 |
| / | 나누기 | x4 = x/y | 2 |
| + | 더하기 | x5 = x+y | 3 |
| - | 빼기 | x6 = x-y | 3 |
3. 함수
함수를 이용하여 변수를 생성할 수도 있다. SAS에서 쓰이는 함수는 이 사이트에 자세히 나와 있으니 참고하자.
[ RAND Function ]
우리가 작성해야 할 프로그램은 무작위 확률 분포에서 sampling을 해야 한다. sampling을 위해 우리는 DO Loop 내에서 RAND 함수를 사용할 것이다. RAND 함수는 난수를 생성하는 함수이다. 이번 프로그램에서 관찰할 분포를 위해 사용할 RAND 함수 문법을 정리하면 아래와 같다.
RAND('BERNoulli', prob) // where (0 ≤ prob ≤ 1), Bernoulli Distribution
RAND ('BINOmial', prob, trials) // where (0 ≤ prob ≤ 1) and (trials ≥ 0)
// Binomial DistributionRAND 함수의 첫 번째 인수는 분포의 이름이다. 분포 이름은 따옴표로 묶어야 한다.
다음 인수 집합은 해당하는 특정한 분포에 대한 매개변수가 차례로 온다.
[ PROC PRINT(테이블 보여주기) ]
테이블 데이터를 보여준다.
- 명령어 정리
PROC PRINT DATA=xxx; // xxx라는 DATA를 불러와 PRINT Procedure를 시행한다.
VAR yyy; // 지정된 변수 yyy를 불러온다.[ 동전 던지기 분포에서 데이터를 생성하고 표본 평균(xbar)을 구하는 프로그램 ]
위의 개념들을 토대로 동전 던지기 분포에서 데이터를 생성하고 표본 평균(xbar)을 구하는 프로그램을 작성했다.
DATA bern;
n=1000000; /* 동전 던지기에서 앞면이 나올 확률을 샘플 1백만개로 추정 */
xsum=0; /* 앞면이 나올 때를 counting 하는 변수. 앞면이 나오면 1,
뒷면이 나오면 0으로 하여 앞면이 몇 번 나오는지 더함 */
p=0.5; /* 앞면이 나올(성공) 확률 = 0.5로 지정. */
DO i=1 TO n;
x=RAND('BERNoulli', p);
/* 던지는 시행을 난수 생성으로 구현 */
xsum=xsum+x; /* 앞면이 나올 때를 counting */
END;
xbar=xsum/n; /* 수학적 확률 구함 */
RUN;
PROC PRINT DATA=bern;
VAR n xbar;
RUN;베르누이 분포(동전 던지기 분포)에서 앞면(성공)이 나올 확률을 p=0.5로 하여 100만개의 베르누이 분포 샘플을 얻고 표본 평균을 구하는 프로그램이다. 이 프로그램을 실행하면 아래와 같은 결과를 얻을 수 있다.

샘플 수(n)이 늘어나게 되면 Loop를 도는 데 시간이 더 오래 걸리기 때문에 프로그램 실행 시간 자체는 증가하지만, 확률의 추정치는 true mean로 수렴(converge)한다.
※ DO Loop 시작 전 xsum=0;을 하는 이유 ( = 변수 초기화를 하는 이유)
프로그램에서 변수가 선언되면 메모리의 빈 공간에 변수 타입에 알맞은 크기의 저장 공간이 확보되고, 이러한 저장 공간은 '변수 이름'을 통해서 사용하게 된다. 그런데 여기서 메모리는 운영체제도 사용하고, A 프로그램도 사용하고, B 프로그램도 사용하는 공유 자원이기 때문에 쓰레기 값(남들이 쓰다가 남은 데이터들)이 들어있을 수 있다.
따라서 변수를 선언할 때 초기화를 하지 않고 사용하게 되면, 메모리에 남아 있는 쓰레기 값이 산출될 수 있기 때문에, 어떤 프로그래밍을 하든 변수 작성을 할 때는 초기화를 필수로 하는 것이 좋다.
[ DO Loop 문을 2개 작성하여 동전 던지기 분포에서 데이터를 생성하고 표본 평균(xbar)을 구하는 프로그램 작성 ]
두 번째로는 샘플 수에 따른 표본 평균의 추정치를 관찰할 수 있게 하기 위하여 DO Loop 문 두 개를 작성하여 동전 던지기 분포에서 데이터를 생성하고 표본 평균(xbar)을 구하는 프로그램을 작성했다.
DATA bern;
n=10000000;
p=0.5; /* 앞면이 나올(성공) 확률 = 0.5로 지정. */
DO i=1000000 TO n BY 1000000;
/* 100만부터 1000만까지 100만씩 증가하는 반복문 */
xsum=0; /* 앞면이 나올 때를 counting 하는 변수. 앞면이 나오면 1,
뒷면이 나오면 0으로 하여 앞면이 몇 번 나오는지 더함 */
DO j=1 TO i;
x=RAND('BERNoulli', p);
/* 던지는 시행을 난수 생성으로 구현 */
xsum=xsum+x; /* 앞면이 나올 때를 counting */
END;
xbar=xsum/i; /* 수학적 확률 구함 */
OUTPUT;
END;
RUN;
PROC PRINT DATA=bern;
VAR i xbar;
RUN;베르누이 분포(동전 던지기 분포)에서 앞면이 나올(성공) 확률을 p=0.5로 하여 베르누이 분포 샘플을 얻고, 시도 횟수(100만 단위)에 따른 평균을 구하는 프로그램이다. 100만 단위로 시행을 하여, 시행의 횟수는 1000만까지 증가하므로 표본 평균은 100만부터 1000만까지 총 10번 출력이 될 것이다. 이 프로그램을 실행하면 아래와 같은 결과를 얻을 수 있다.

샘플 수를 더 많아지게 하면, 표본 평균(xbar)는 점점 true mean=0.5에 수렴하게 된다. 즉, 샘플이 많으면 우리의 추정치가 true mean에 수렴한다는 것을 확인할 수 있다.
'Language > SAS' 카테고리의 다른 글
| [ SAS ] - 평균 회귀 모형에서 기초 통계량을 추출하는 프로그램 작성 + 가설 검정 (0) | 2023.04.21 |
|---|---|
| [ SAS ] - 정규 분포에서 기초 통계량을 추출하는 프로그램 작성 (0) | 2023.04.15 |
| [ SAS ] - 이산 확률 분포에서의 확률을 구하는 프로그램 작성 (0) | 2023.04.07 |
| [ SAS ] - DATA를 입력하고, sorting하는 프로그램 작성 (0) | 2023.03.20 |
| [ SAS ] - 언어에 대한 소개 및 SAS Studio 설치 방법 (4) | 2023.03.16 |





댓글 영역